Bonjour à tous,
Voici, un petit problème de géométrie auquel je n'ai jamais trouvé la solution.
On a un point D à l'intérieur d'un triangle équilatéral ABC.
De sorte que,
AD=5cm
BD=4cm
CD=3cm
Quel est l'aire du triangle ABC ?
Merci de votre aide.
Petit problème de géométrie
9 messages
- Page 1 sur 1
Re: Petit problème de géométrie
Avec la formule de Héron, peut-être.
Nomme a la mesure de chaque côté de ABC.
Nomme a la mesure de chaque côté de ABC.
Re: Petit problème de géométrie
Salut,
Si on a un triangle équilatéral de coté
de coté  et un point
et un point  tel que
tel que  ,
,  et
et  alors
alors
(a\!+\!b\!-\!c)(a\!-\!b\!+\!c)(-a\!+\!b\!+\!c)})
A toi de jouer...
Si on a un triangle équilatéral
A toi de jouer...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Petit problème de géométrie

Il semble qu'une méthode assez simple consiste à placer l'image de D par la rotation de centre A qui transforme B en C. J'ai bêtement nommé cette image E'.
On se retrouve comme par hasard avec un triangle rectangle DCE'.
Pour avoir AC², il n'y a qu'à utiliser le théorème d'Al Kashi dans ACE'.
L'angle AE'C est la somme d'un angle de 60° et d'un angle dont on a le sinus et le cosinus avec le triangle rectangle.
On arrive à une aire de
Si, au lieu de 5, 4, 3, on prend 5, 4 ,2, on y arrive aussi puisqu'on peut avoir le cosinus avec Al Kashi.
On arrive à une aire de

Re: Petit problème de géométrie
Merci pour ces réponses,
Les trois semblent donner le même résultat (heureusement )
)
Mais, je trouve la dernière beaucoup plus élégante.
Ben314 pourrais tu me dire d'où tu sors cette formule:
Les trois semblent donner le même résultat (heureusement
Mais, je trouve la dernière beaucoup plus élégante.
Ben314 pourrais tu me dire d'où tu sors cette formule:
Ben314 a écrit:
Re: Petit problème de géométrie
J'y suis allé totalement à la bourrin :
Si tu écrit que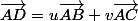 alors
alors
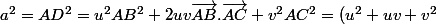x^2) donc
donc ^2=u^2+uv+v^2\ (E_1))
De même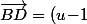\vec{AB}+v\vec{AC}) implique que
implique que ^2=(u\!-\!1)^2+(u\!-\!1)v+v^2\ (E_2))
De même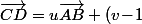\vec{AC}) implique que
implique que ^2=u^2+u(v\!-\!1)+(v\!-\!1)^2\ (E_3))
Ensuite, et
et  te donnent deux équations linéaires en
te donnent deux équations linéaires en  et
et  (à coefficients "réellement" constant) qui te permettent de les déterminer en fonction de
(à coefficients "réellement" constant) qui te permettent de les déterminer en fonction de  et il n'y a plus qu'à réinjecter ça dans n'importe laquelle des 3 pour obtenir une équation bicarré en
et il n'y a plus qu'à réinjecter ça dans n'importe laquelle des 3 pour obtenir une équation bicarré en  dont la solution est celle ci dessus et dans laquelle apparait "magiquement" la formule de Héron donnant la surface du triangle de cotés
dont la solution est celle ci dessus et dans laquelle apparait "magiquement" la formule de Héron donnant la surface du triangle de cotés  (le terme avec la racine).
(le terme avec la racine).
EDIT :
En fait, si on note la surface du triangle équilatéral (ABC),
la surface du triangle équilatéral (ABC),  les surfaces des trois triangles équilatéraux de cotés respectifs
les surfaces des trois triangles équilatéraux de cotés respectifs  et
et 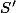 celle du triangle de cotés
celle du triangle de cotés  , alors on a :
, alors on a :
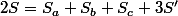
Et ça se "lit" directement sur une figure sur laquelle on fait 3 rotations comme celle de chan79 pour faire apparaitre à la fois et
et  (le triangle ACA' est isométrique à ABD, idem pour les deux autres et ça explique que la surface totale coloriée soit le double de celle du triangle ABC)
(le triangle ACA' est isométrique à ABD, idem pour les deux autres et ça explique que la surface totale coloriée soit le double de celle du triangle ABC)

Si tu écrit que
De même
De même
Ensuite,
EDIT :
En fait, si on note
Et ça se "lit" directement sur une figure sur laquelle on fait 3 rotations comme celle de chan79 pour faire apparaitre à la fois

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Petit problème de géométrie
Bonjour à tous
C'est un problème qui revient trop souvent avec des côtés 345 pour faire son Pythagore
Quelques exemples de solutions http://www.forum.math.ulg.ac.be/viewthread.html?SESSID=c556c43f9d1dbc7368c72d9dcba46d1d&id=54143
J'en ai proposé deux vers la fin .
Imod
C'est un problème qui revient trop souvent avec des côtés 345 pour faire son Pythagore

Quelques exemples de solutions http://www.forum.math.ulg.ac.be/viewthread.html?SESSID=c556c43f9d1dbc7368c72d9dcba46d1d&id=54143
J'en ai proposé deux vers la fin .
Imod
Re: Petit problème de géométrie
La démonstration mise plus haut se généralise.

Al Kashi dans DBD':
=a^2+b^2-c^2)
soit
=(a^2+b^2-c^2)^2)
on pose:=m^2)
Par addition:
^2 +m^2)
^2-(a^2+b^2-c^2)^2)
on arrive à
(a+b+c)(a-b+c)(-a+b+c))
=\frac{\sqrt{(a+b-c)(a+b+c)(a-b+c)(-a+b+c)}}{2ab})
Al Kashi dans ACD':
-\frac{\sqrt{3}}{2}sin(\alpha )))
(a+b+c)(a-b+c)(-a+b+c)}))
(a+b+c)(a-b+c)(-a+b+c)}))
L'aire de ABC est
+3 \sqrt{(a+b-c)(a+b+c)(a-b+c)(-a+b+c) } \ ))
A noter que la quantité sous la racine est bien toujours positive car si un point est situé à l'intérieur d'un triangle équilatéral, sa distance à l'un des sommets est inférieur ou égale à la somme de ses distances aux deux autres sommets.

Al Kashi dans DBD':
soit
on pose:
Par addition:
on arrive à
Al Kashi dans ACD':
L'aire de ABC est
A noter que la quantité sous la racine est bien toujours positive car si un point est situé à l'intérieur d'un triangle équilatéral, sa distance à l'un des sommets est inférieur ou égale à la somme de ses distances aux deux autres sommets.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
