Géométrie - Aide
Olympiades mathématiques, énigmes et défis
-
Alcane
- Messages: 2
- Enregistré le: 22 Jan 2016, 18:15
-
 par Alcane » 22 Jan 2016, 18:31
par Alcane » 22 Jan 2016, 18:31
Bonjour à tous,
Je dois résoudre un problème de géométrie mais je bloque:
Énoncé:
On sait que: AB =AC
et AD = BC = CE = DE
Question: angles BAC = ?

Je pense qu'il faut le démontrer avec les angles et triangles isocèles mais je ne vois pas comment

Merci à ceux qui prendront le temps de m'aider

Stéphane.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Jan 2016, 19:55
par Ben314 » 22 Jan 2016, 19:55
Un grand grand grand classique parmi les problèmes de géométrie (compliqués) : l'Octadécagone (polygone régulier à 18 cotés)

Reste à vérifier que c'est bien ta figure qui est représentée ci dessus (dans laquelle on lit aisément tout les angles).
P.S.1 : Merçi Imod (il comprendra s'il passe par là...)
P.S.2 : Il peut être intéressant de trouver une preuve que l'angle en question vaut 100° sans passer par l'Octadécagone, mais il est quasi-sûr qu'il faudra construire des points supplémentaires qui sont "naturels" sur l'Octadécagone. Je chercherais si j'ai un peu de temps...
(On peut évidement le faire aussi avec de l'analyse, c'est a dire de la trigo et/ou un repère, mais c'est en général une solution considérée comme "peu esthétique")
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Alcane
- Messages: 2
- Enregistré le: 22 Jan 2016, 18:15
-
 par Alcane » 22 Jan 2016, 22:29
par Alcane » 22 Jan 2016, 22:29
Oulalalala
Merci beaucoup pour ta réponse, j'aurai jamais trouvé par moi-même... je pensais qu'il faisait 90° haha.
Je pensais pas que c'était aussi compliqué, thx!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Jan 2016, 11:57
par Ben314 » 23 Jan 2016, 11:57
Il y a plusieurs problèmes de géométrie connus qui "partent" de l'Octadécagone (j'en connais au moins 4 ou 5) et qui sont tous extrêmement difficile si on ne construit pas le polygone, en particulier du fait que les angles de 10° et 20° qui apparaissent forcément sur la figure sont "peu classique" (et avec des sinus et des cosinus bien pourris...)
Après, c'est Imod (un autre intervenant du forum qui est féru de jolis problèmes de géométrie) qui m'avait donné "le truc" : dés qu'on constate (par exemple avec géogébra) que la figure à étudier contient de tels angles, il faut chercher un Octadécagone dans lequel la figure est inscrite et ça fait passer le niveau de ces problèmes de "extrêmement difficile" à "relativement simple" (c'en est presque triste...)
Sinon, as tu réussi a montrer que la figure du post précédent vérifie bien les hypothèses de ton problème ?
(Il faut aussi que tu montre que la figure est "unique", mais en général, ce n'est pas très compliqué)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Jan 2016, 11:34
par chan79 » 24 Jan 2016, 11:34
salut
une autre approche:

on pose AE=2
a: angle DEA
I milieu de AE
J milieu de BC
tan(a)=AI/1=AI
Avec Pythagore: DE²=1+tan²a
Donc DE=1/cos(a)
Comme DE=CE, on a AC=(1/cos(a))-2
L'angle ACJ=a/2
on pose d=BC
=\frac{\frac{d}{2}}{\frac{1}{cos(a)}-2})
Comme CB=CE=DE
\times (\frac{1}{cos(a)}-2})=\frac{1}{cos(a)})
(1-2 cos(a))=1)
or, on sait que
=2cos^2 (\frac{a}{2})-1)
en posant t=cos(a/2) on arrive à:
=1)
soit

soit
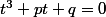
avec p=-3/4 et q=1/8
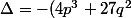=\frac{81}{64})
trois solutions réelles
+\frac{k2\pi}{3}))
avec k=0,1,2
soit cos(2pi/9+k2pi/3)
et on trouve que la solution qui convient est cos(2pi/9)=cos(40°)
a/2=40°
a=80°
L'angle cherché est 180°-80°=
100°l'idée est donc d'exprimer d=BC en fonction de l'angle a, ce qui permet de poser l'équation puisque d=CE.
Il y a quelques calculs (qui s'arrangent bien !) mais ça ne fait pas de mal ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Jan 2016, 15:13
par Ben314 » 24 Jan 2016, 15:13
A mon avis, tant qu'à faire de le faire "à la bourrin", ça serait quand même plus malin de prendre comme inconnue un angle "simple", par exemple l'angle

(qui vaut 30°).
Une petite "chasse aux angles" dans les différents triangles isocèles montre que b=90°-3a/4 (avec ton a) donc que a=120°-4b/3 et ton "équation caractéristique"
\big(1\!-\!2\cos(a)\big)\!=\!1)
devient
\!-\!6\cos(\frac{2b}{3})\!=\!1)
.
Or, MIRACLULEUSEMENT,
\!=\!4\cos^3(\theta)\!-\!3\cos(\theta))
et l'équation devient tout simplement
=1)
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Jan 2016, 15:23
par chan79 » 24 Jan 2016, 15:23
Ben314 a écrit:A mon avis, tant qu'à faire de le faire "à la bourrin", ça serait quand même plus malin de prendre comme 1[/tex].
oui, on peut toujours trouver mieux mais tu devrais faire preuve de moins de suffisance.
C'est si difficile d'être un peu agréable ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Jan 2016, 00:16
par Ben314 » 25 Jan 2016, 00:16
J'ai pas l'impression d'être franchement désagréable en général (si ?).
Mais là, à mon sens, tu cherche quand même "le bâton pour te faire battre" : non seulement tu propose une solution calculatoire à un (joli) problème de géométrie (ce qui pour moi est déjà une "faute de gout" assez marquée), mais en plus la solution fait intervenir des équations du 3em degré qu'on sait être en général non "résoluble géométriquement" (donc les truc dont on parle risque de "ne pas exister" géométriquement) et, cerise sur le gâteaux, elle ne prend très clairement pas les bonnes inconnues au départ (ce qui permettrait au moins d'éviter une partie du "gros bourrinage").
Tu trouve pas que ça fait un peu beaucoup ?
Après, si c'est un problème style relation humaine ou du même acabit et que tu trouve que je t'ai "mal parlé", c'est totalement involontaire et je m'en excuse platement et extrêmement humblement.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité




