Exercice vecteur (1r S)

[clems93]

bonsoir, j'ai un Exercice noté pour demain, je suis naz en maths et je bloque vraiment...

aidez moi svp
merci

soit ABCD un parrallelogramme, I le milieu de [AB] et le point E défini par : vecteur IE = 1/3 ID (vecteur).

1) exprimiez les vecteurs AC et AE dans la base (AB vecteur, AD vecteur)
2) En déduire que les points A, E et C sont alignés.

[Imod]

Utilise la relation de Chasles .

Imod

[matteo182]

Salut,
Alors je vais tenter d'apporter un élément de réponse à tes questions.
Tout d'abord exprimer un vecteur dans une base, cela veut dire qu'il faut l'écrire comme combinaison linéaire de ces vecteurs, autrement dit ici, en fonction de et .

En utilisant la règle du parallelogramme pour les vecteurs on a donc facilement que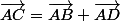 . C'est gagner pour .

Ensuite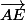 est un peu plus compliqué. Décomposons le d'abord avec la règle de Chasles : 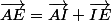. I étant milieu de AB, on a 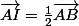et comme 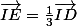on a :
.
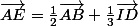Ensuite On Ré-Utilise la relation de Chasles pour décomposer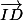 , ie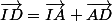
et on injecte ceci dans l'égalité précédente :
.
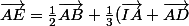Ensuite développe tout ca, remarque que .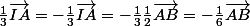
En faisant la somme de tout ce qu'il te reste, tu dois trouver :
.

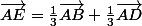Pour voir que les points sont alignés il suffit d'utiliser l'expression de trouvée plus haut et de l'injecter dans l'expression de 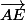et tu dois avoir 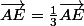ce qui prouve que les points A, E et C sont alignés.

Ce fut long mais pas si compliqué
Bonne Soirée

[matteo182]

Petite Erreur de frappe, dernière ligne il fallait lire :
.

[Imod]

Merci matteo182 , notre auteur n'a plus qu'à recopier la solution . Je persiste à croire que l'on apprend les mathématiques par la pratique et que fournir une solution complète à un élève toujours désespéré , nul en math bien sûr , mais en S tout de même ( ?????) et sans doute peu courageux , ne fait rien d'autre qu'encourager la paresse et n'aide personne . A part recopier le sujet , l'auteur a-t-il apporté un seul élément de réponse ?

Imod