Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Polytechnique enp » 29 Déc 2015, 20:45
par Polytechnique enp » 29 Déc 2015, 20:45
Salut tt le monde comment calculer
L'intégrale de ;)((x-a)(b-x)) dx a,b dans R

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Déc 2015, 20:52
par zygomatique » 29 Déc 2015, 20:52
salut
déjà il faut que (x - a)(b - x) >= 0 ....
or
(b - x) = (a + b)^2/4 - [x - (a + b)/2]^2)
puis faire le changement de variable u = .....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 29 Déc 2015, 21:14
par aymanemaysae » 29 Déc 2015, 21:14
je crois que c'est
}^2)
-
}^2)
.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 29 Déc 2015, 21:20
par jlb » 29 Déc 2015, 21:20
Polytechnique enp a écrit:Salut tt le monde comment calculer
L'intégrale de

((x-a)(b-x)) dx a,b dans R
bonsoir, tu as essayé y=;)((x-a)(b-x)) comme chgt de variable? à vérifier mais cela a l'air de bien se simplifier.
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 29 Déc 2015, 21:22
par jlb » 29 Déc 2015, 21:22
Polytechnique enp a écrit:Salut tt le monde comment calculer
L'intégrale de

((x-a)(b-x)) dx a,b dans R
Bonsoir, as-tu essayé le chgt y=;)((x-a)(b-x)) ? A vérifier, cela a l'air de bien se simplifier avec très peu de calculs.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 29 Déc 2015, 21:23
par MouLou » 29 Déc 2015, 21:23
Si je me souviens bien il faut essayer de se ramener à (x-1)(x+1) avec un bon chgt de variable
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 29 Déc 2015, 22:03
par MouLou » 29 Déc 2015, 22:03
Alors oui j'ai un truc un peu tortueux, tout le but étant de me ramener à l'intégrale de -1 à 1 de
(1-u)}=\sqrt{1-u^{2}})
, que je sais calculer avec le chgt de variable u=cost ou u=sint.
Bon déjà faut préciser dans quoi on veut intégrer. Le domaine de définition ici c'est a<x<b (on suppose a<b).
Ensuite je cherche un changement de variable affine

qui envoie a sur -1 et b sur 1. et le miracle c'est que j'envoie x-a sur u+1 et b-x sur b-u à facteur multiplicatif près.
Ensuite après ce changement de variable je me retrouve à un facteur multiplicatif près à l'intégrale que je sais calculer.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 29 Déc 2015, 22:17
par Pisigma » 29 Déc 2015, 22:17
Polytechnique enp a écrit:Salut tt le monde comment calculer
L'intégrale de

((x-a)(b-x)) dx a,b dans R
Bonsoir,
C'est une primitive ou une intégrale que tu cherches. Si c'est une intégrale, il manque les bornes.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Déc 2015, 23:11
par Ben314 » 29 Déc 2015, 23:11
Salut,
Si par hasard le truc que tu as à calculer c'est
(b-x)})
avec a<b, personnellement, je t'inciterais surtout à faire un dessin vu que cette intégrale se calcule... sans calculs...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Déc 2015, 01:44
par Ben314 » 30 Déc 2015, 01:44
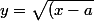(b-x)}\ \Leftrightarrow\ y^2+x^2-(a+b)x+ab=0\text{ et }y\geq 0\ \Leftrightarrow\ \big(x-\frac{a+b}{2}\big)^2+y^2=\big(\frac{b-a}{2}\big)^2\text{ et }y\geq 0)
Donc le graphe de

est le demi-cercle de diamètre [AB] (au dessus de l'axe des x) où A:(a,0) et B:(b,0) et on en déduit que l'aire sous la courbe est
^2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 30 Déc 2015, 11:50
par MouLou » 30 Déc 2015, 11:50
Jolie facon de faire!

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Déc 2015, 13:53
par zygomatique » 30 Déc 2015, 13:53
ha oui bien vu ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 31 Déc 2015, 22:16
par aymanemaysae » 31 Déc 2015, 22:16
C'est une très astucieuse méthode.
Pour en faire profiter un large éventail d'étudiants et d'élèves en CPGE, je vous demande la permission de l'éditer sur un autre
site, bien sûr en respectant les droits d'auteur: en plus, je ne sais pas si c'est permis d'éditer aussi les références de votre site
(http://www.maths-forum.com) .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
(1-u)}=\sqrt{1-u^{2}}) , que je sais calculer avec le chgt de variable u=cost ou u=sint.
, que je sais calculer avec le chgt de variable u=cost ou u=sint. qui envoie a sur -1 et b sur 1. et le miracle c'est que j'envoie x-a sur u+1 et b-x sur b-u à facteur multiplicatif près.
qui envoie a sur -1 et b sur 1. et le miracle c'est que j'envoie x-a sur u+1 et b-x sur b-u à facteur multiplicatif près.