aleba a écrit:Bonsoir,
J'ai besoin d'un complément d'information au sujet du développement de la factorisation d'une équation du 2eme degré.
Prenons : ax²+bx+c=0
On factorise avec a : a(x²+b/a*x+c/a)=0
On utilise la 1ere identité remarquable (a+b)²=(a+b)(a+b)=a²+ab+ba+b²=a²+2ab+b²
Pour y arriver, on multiplie et divise par 2 le terme central : a(x²+2*b/2a*x+c/a)=0
Ensuite, on ajoute et on soustrait le nombre b²/4a² : a(x²+2*b/2a*x+b²/4a²-b²/4a²+c/a)=0
On factorise et on simplifie : a(x²+2*b/2a*x+(b/2a)²) -b²/4a²+4ac/4a²)=0
a((x+b/2a)² -(b²-4ac)/4a²)=0
=> c'est là que je bloque, pourquoi -(b²-4ac)/4a²]? Pourquoi pas -(4ac-b²)/4a² ?
On utilise la 1ere identité remarquable (a+b)²=(a+b)(a+b)=a²+ab+ba+b²=a²+2ab+b²
une identité remarquable n'a pas besoin d'être établie à nouveau. Elle est supposée connue
Ton cheminement dans la démo. fait penser à une recette de cuisine !
Le but est de mettre le trinôme sous la forme de la différence de 2 carrés que l'on sait alors factoriser :
Donc on cherche dans

le début d'un carré.
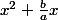
serait bien le début d'un carré si

était un double produit. Qu'à cela ne tienne :

est bien un double produit
et
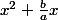
est le début du carré de

:
^2=x^2+\frac{b}{a}x+\frac{b^2}{4a^2})
Le trinôme devient
^2 -\frac{b^2}{4a^2} +\frac{c}{a}])
On réduit au même dénominateur les 2 derniers termes :
^2 -\frac{b^2}{4a^2} +\frac{4ac}{4a^2}]=a[(x-\frac{b}{2a})^2-\frac{b^2-4ac}{4a^2}])
