Barycentre

[valerieprb]

Bonjour, voici la mise en contexte de l’exercice que je suis incapable de compléter ...

Quatre points A,B,C,D sont situés dans un espace tridimensionnel. Dans un certain repère, les coordonnées A,C,D sont connues : A(1,1,1); C(2,0,1); D(0,3,0).

Les coordonnées du barycentre de {A,B,C} sont : (4/3, 1/3, 4/3)

a)Déterminez les coordonnées du point B dans le repère utilisé.
b)Déterminez les coordonnées du barycentre de {A,B,C,D} dans ce même repère.
c) Les points A,B,C sont-ils colinéaires ?
d) Quelle est la distance entre les points A et B ?

Merci à l'avance pour l'aide apportée

[zygomatique]

salut

il suffit d'écrire mathématiquement (vectoriellement) ce que signifie que G(4/3, 1/3, 4/3) est le barycentre des points A, B et C ....

[aymanemaysae]

Peut-on parler de barycentre sans que les points en question ne soient pondérés?

[zygomatique]

ben le poids est 1 ....

[valerieprb]

Regarder, j'ai trouvé en a) les coordonnées de B=(1,0,2)

[valerieprb]

Déterminez les coordonnées du barycentre de {A,B,C,D} dans ce même repère.

C'est là que ça se corse ...

[zygomatique]

ben c'est la même chose ...

on peut toujours nommer O l'origine du repère ....

PS : je ne vérifie pas tes calculs ....

[aymanemaysae]

N'érigez pas une montagne devant vous avant d'avoir commencé: ça devient plutôt simple, vous n'avez qu'à suivre les conseils e M. Zygomatique.
Je viens de lire votre message M. Zygomatique: les coordonnées de B sont justes.

[valerieprb]

B = ((1+b1+2/3),(1+b2+0/3),(1+b3+1/3)) = (4/3, 1/3, 4/3) si et seulement si B=(1,0,2)

[zygomatique]

ok ... ça semble correct ....

on fait donc la même chose avec les quatre points A, B, C et D ...

[aymanemaysae]

Pour la deuxième question,on a :
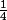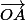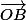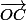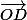(+++)= : avec G' le barycentre de ABCD.

Quant à la troisième question, il faut voir si les vecteurs et sont colinéaires, ou bien remarquer que les points B et C appartiennent au plan xOz càd que toutes les droites contenant B et C se trouvent dans ce plan, alors que A non.

Et en ce qui concerne la quatrième question, il faut calculer la racine carrée de la norme du vecteur .