Fonctions (DM T ES)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 13:15
par Bob45 » 28 Sep 2006, 13:15
Voila, j'ai vraiment essayer de comprendre mais rien a faire, je pige pas, regardez et dites moi si vous pouvez m'aider. (je suis en T ES)
Sur l'intervalle I = [0 ; 13], on a la fonction f définie par:
f(x) = x³ - 21x² + 120 -100 / 27
Ce que j'ai trouvé: f(4)=4 f(13)=4
Question où je suis bloqué: Vérifier par le calcul que ces valeurs lues sont bien solutions de l'équation f(x)=4
Il faut dériver non? Pouvez vous m'expliquez?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Sep 2006, 13:29
par fonfon » 28 Sep 2006, 13:29
Salut, f(x)=4 il suffit que tu resolves
ce qu'on te donne pour la fonction =4 je n'ai pas marqué la fct car je pense qu'il manque un x à 120 et je sais pas si /27 c'est pour tout ou juste pour 100 il faudrait des parenthèses
finallement je viens de le faire il faut que tu resolves

-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 13:31
par Bob45 » 28 Sep 2006, 13:31
Je m'étais trompé...
ben j'ai essayé mais j'y suis pas arrivé du tout.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Sep 2006, 13:42
par fonfon » 28 Sep 2006, 13:42
re,
donc:
=4})



d'apres ce que tu as trouvé graphiquement tu peux te dire que x=4 est racine de x^3-21x²+120x-208 donc factorisable par (x-4)
donc
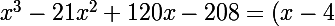(ax^2+bx+c))
donc soit que tu fais une identification pour trouver a,b,c sinon tu fais la division de x^3-21x^2+120x-208 par (x-4)
essaies de poursuivre
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 14:00
par Bob45 » 28 Sep 2006, 14:00
Houla ça a pas l'air simple, je vais voir ça de suite!
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Sep 2006, 14:05
par fonfon » 28 Sep 2006, 14:05
il suffit que tu developpes (x-4)(ax²+bx+c) et ensuite tu identifies les different coefficients des termes de même degrè les x^3 avec les x^3 ,les x² avec les x² ...
ou bien tu fais la division
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 14:49
par Bob45 » 28 Sep 2006, 14:49
Je trouve quelques chose n'ayant aucun sens... :triste: Je suis désespéré.
Tu vois comment faire?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Sep 2006, 15:24
par fonfon » 28 Sep 2006, 15:24
donc me voilà j'été parti
(ax^2+bx+c)}=ax^3+bx^2+cx-4ax^2-4bx-4c=ax^3+x^2(b-4a)+x(c-4b)-4c)
or
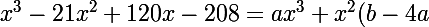+x(c-4b)-4c)
donc il reste plus qu'a identifier les termes de même degré de part et d'autre donc on obtient un systeme:


donc
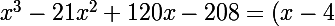(x^2-17x+52))
reste a chercher les racines de (x^2-17x+52) et de regarder si tes valeurs de x que tu as lu sur le graphique sont les mêmes.
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 16:26
par Bob45 » 28 Sep 2006, 16:26
Quand je remplace X par 4 ou 13 dans l'équation que tu trouves a la fin, je ne trouve pas une égalité, est ce normal ou pas? :hein:
mon adresse e-mail si cela ne t'embête pas de me parler par msn:
bob45-paradise@hotmail.fr
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Sep 2006, 16:34
par fonfon » 28 Sep 2006, 16:34
re, je te repondrais tout à l'heure si tu veux sur msn si tu ne comprends pas ce qui suit car là je m'en vais sinon qd tu as chercher les racines de x²-17x+52 tu as trouvé 4 et 13 je suppose donc:
(x-4)(x-13)=(x-4)^2(x-13))
donc
=4})

^2(x-13)=0)

ou

donc f(x)=4 ssi x=4 ou x=13
donc tu as bien demontrer ce que tu cherchais à savoir que f(4)=4 et f(13)=4
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 16:44
par Bob45 » 28 Sep 2006, 16:44
J'ai tout compris ce que tu as mis mais j'ai toujours pas saisi quelques petits trucs. Merci pour l'instant de ton aide. :we:
-
Sinople
- Messages: 1
- Enregistré le: 28 Sep 2006, 16:32
-
 par Sinople » 28 Sep 2006, 18:13
par Sinople » 28 Sep 2006, 18:13
euh j'ai le même probléme que bob 45 mais je ne comprend pas vraiment vos explications
N'y aurait il pas une méthode plus simple car je n'arrive pas a comprendre comment vous avez fait.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 28 Sep 2006, 18:15
par fonfon » 28 Sep 2006, 18:15
Salut, c'est le même exo?
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 28 Sep 2006, 20:04
par Bob45 » 28 Sep 2006, 20:04
Oui il a le même que moi car il est dans ma classe!
Peut tu remettre la méthode pour trouver delta stp et expliquer un peu?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 29 Sep 2006, 07:27
par fonfon » 29 Sep 2006, 07:27
Salut, une equation du second degré est de la forme ax²+bx+c(a#0) Les eventuelles solutions de l'equation sont aussi appelées racines ou zeros du polynôme.
on pose

(appelé discriminant du trinôme)
Si
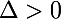
l'equation admet 2 solutions distinctes:
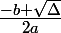
ou
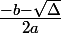
Si
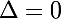
l'equation a une solution double:

Si

l'equation n'a pas de solution réelle, mais admet 2 solutions complexes (nombres complexes)
donc voilà
-
Bob45
- Membre Relatif
- Messages: 130
- Enregistré le: 28 Sep 2006, 13:03
-
 par Bob45 » 01 Oct 2006, 20:30
par Bob45 » 01 Oct 2006, 20:30
bonsoir! Comment faire passer cela -1 (x-7)+2 a cette forme d'opération: ax²+bx+c
c'est possible? répondez vite please
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
(x-4)(x-13)=(x-4)^2(x-13))
=4})

^2(x-13)=0)
 ou
ou 
 (appelé discriminant du trinôme)
(appelé discriminant du trinôme)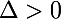 l'equation admet 2 solutions distinctes:
l'equation admet 2 solutions distinctes: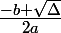 ou
ou 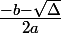
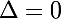 l'equation a une solution double:
l'equation a une solution double:
 l'equation n'a pas de solution réelle, mais admet 2 solutions complexes (nombres complexes)
l'equation n'a pas de solution réelle, mais admet 2 solutions complexes (nombres complexes)