Intégration par partie

[Vados]

Bonsoir à tous , je dois réaliser l'intégration par partie de (x²-1)e^3x , entre -1 et 1 ...

Je voudrais juste savoir si mon résultat est correcte , et si non m'aider pour le résoudre :

(-2e^3 / 3) - (2e^-3 / 3 )

[chan79]

Salut
ton résultat devrait être proche de -2,99
A priori, deux IPP successives
pour la première
u=x²-1
v'=

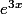
[Vados]

Pour moi v'=e^3x
Donc u'=2x et v=e^3x / 3

[chan79]

Pour moi v'=e^3x
Donc u'=2x et v=e^3x / 3

c'est ça; continue

[Vados]

Du coup [u'v] - [uv']

donc [(2x)*(e^3x / 3)] - [(x²-1)*(e^3x)]

Deja [(x²-1)*(e^3x)] , pour -1 ou 1 , on aura bien 0 car (x²-1) = 0

Et sinon je trouve (2e^3 / 3) - (2e^-3 / 3 )

[chan79]

Mets le détail; ça ne colle pas

[Vados]

Ben je remplace u'v par 1 et par -1

[aymanemaysae]

Pour récapituler le travail des autres correcteurs que je salue ici leur abnégation, et pour nous permettre à M. Vados et moi de comparer les résultats de notre travail, je soumets à votre bienveillance l'intégralité de ma solution qui je l'espère est exempte d'erreurs, sinon je serai très honoré de lire vos remarques:

[zygomatique]

salut

soit u une fonction affine et P un polynome de degré n ...

alors il existe un polynome Q de même degré n que P tel que Q(x)exp(u(x)) soit une primitive de P(x)exp(u(x))

... si on ne veut pas faire d'IPP

:lol3:

[aymanemaysae]

Merci M. Zygomatique, vraiment c'est une très bonne méthode.

[Vados]

Merci beaucoup pour votre aide mais je ne comprend pas d'ou sort le 1/3 ...

[aymanemaysae]

M. Vados, Je n'ai donné que la méthode et pas la solution, car moi j'ai travaillé avec e-3x et non avec e3x, d’où la différence de signe: la primitive pour vous sera ((9x^2 -6x -7)/27)e3x mais le résultat restera le même.