Salut,
J'étudie les logarithmes et je suis tombé sur ce problème:
"Début 2013, un chercheur américain de l'université du Missouri, Curtis Cooper, rapporte la découverte du plus grand nombre premier jamais trouvé : 2^57885161 -1. Combien ce nombre a-t-il de chiffres ?"
En fait je ne vois pas en quoi les logarithmes peuvent aider à le résoudre.
Logarithmes
5 messages
- Page 1 sur 1
Logarithme décimal
On pose =\frac{Ln(x)}{Ln(10)})
on a
=0)
=1)
=n log(10)=n)
si un entier N possède n chiffres

E() désigne la partie entière d'un réel.
le log étant croissant
 < n)
d'où)=n-1)
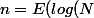)+1)
conclusion : le logarithme décimal d'un entier est , peu ou prou, son nombre de chiffres en base 10
on a
si un entier N possède n chiffres
E() désigne la partie entière d'un réel.
le log étant croissant
d'où
conclusion : le logarithme décimal d'un entier est , peu ou prou, son nombre de chiffres en base 10
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
