Exercice logarithmes

[tomtom21]

Bonjour, j'ai un exercice à faire sur des logarithmes mais je suis totalement bloqué.

Voici l'énoncé : " La magnitude apparente d'un astre d'éclat E est définie à partir d'un éclat de référence par . La convention est que la magnitude augmente de 5 lorsque l'éclat est divisé par 100".

1/ Calculer
2/ Déterminer la magnitude apparente des astres suivants :



Je n'ai pas du tout compris ce qu'il fallait faire dans la question 1.
La question étant simplement des applications numériques, je l'ai facilement réussis et j'ai obtenu : et

[mathelot]

Bonjour, j'ai un exercice à faire sur des logarithmes mais je suis totalement bloqué.

Voici l'énoncé : " La magnitude apparente d'un astre d'éclat E est définie à partir d'un éclat de référence par . La convention est que la magnitude augmente de 5 lorsque l'éclat est divisé par 100".

1/ Calculer

quand on divise par 100, d'après les propriétés du log
ça fait une différence de

[tomtom21]

quand on divise par 100, d'après les propriétés du log
ça fait une différence de

Okay je te suis jusque là, mais je ne vois comment répondre à la premiere question avec ce que tu m'as dit... :triste:

[mathelot]

Okay je te suis jusque là, mais je ne vois comment répondre à la premiere question avec ce que tu m'as dit... :triste:

.

[tomtom21]

.

Okay... mais c'est pas "ln(a)" qu'on veut trouver, c'est "log(a)".

Or il n'apparait pas dans la dernière expression que tu as mentionné.

[mathelot]

Okay... mais c'est pas "ln(a)" qu'on veut trouver, c'est "log(a)".

Or il n'apparait pas dans la dernière expression que tu as mentionné.

log(a) n'existe pas. tu as des idées fausses sur cette définitions.

1/Ln(a) est un coefficient multiplicateur du logarithme népérien

[Robic]

Dans ce genre d'exercice il faut être capable de traduire l'énoncé.

« la magnitude augmente de 5 lorsque l'éclat est divisé par 100. »

Traduction :
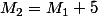
lorsque .

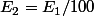
Ensuite il faut utiliser les données de l'énoncé. Il paraît que

Du coup ça donne :

lorsque .

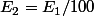
Autrement dit :



Jusque là, je n'ai fait que traduire l'énoncé et utiliser la définition de la magnitude. Bref, je n'ai pas encore vraiment commencé.

Pour la suite, il peut être utile d'écrire sous la forme + quelque chose, sans doute en utilisant la propriété .

À la fin on trouve l'égalité indiquée par Mathelot (je suis moins astucieux que lui, mais je voulais utiliser une démarche systématique : traduire l'énoncé, utiliser les hypothèses). Ça permettra de trouver ln(a) et donc de connaître la base du logarithme qui définit les magnitudes. (Je pense que c'est bien ln(a) qu'il faut trouver, puisqu'il est nécessaire de connaître sa valeur afin de calculer des logarithmes en base a.)

(Pour info, la magnitude apparente du Soleil fait de l'ordre de -27, et celle de la pleine Lune vaut à peu près -12 (si la Lune est en fin croissant, la valeur absolue est plus petite). Si l'exercice utilise des données réalistes, c'est ce genre de valeur qu'il faudra trouver.)

-----
Je viens de terminer les calculs en suivant les indications ci-dessous. Après avoir déterminé ln(a), j'ai calculé la magnitude du Soleil et je trouve -26,69993... ce qui est sans doute correct.

[tomtom21]

Okay, alors bon j'ai bien avancé sur l'exercice, sauf qu'il y a un problème, moi en magnitude du soleil, je trouve +24 (environ) et non pas -24

Et je vois pas où j'ai pu merder ... :/

[Robic]

Est-ce que tu as trouvé ?

Si oui, ça veut dire que .

x vaut par exemple 4,786E+10.

[tomtom21]

Aaaaaaaaaaaaaaaaaaah ça y est... je viens de voir le "moins" qui s'est volatilisé de ma copie entre deux lignes de calcul... :mur:

et pour te répondre, oui j'ai bien le même résultat que toi