Limite / niveau licence 1 MASS

[Nedroma]

Bonjours quelqu´un pourrai m'aider afin de résoudre cette exercice:
Calculer les limite suivantes :
1) lim x->0 [(racine carré 1+x)-1] au carrée le tout divisée par xsinx
2) lim x->0 epx^x-(racine carré 1+x) le tout divisée par x
3) lim x->+ infini sinx/lnx

Je vous remercie

[mrif]

Bonjours quelqu´un pourrai m'aider afin de résoudre cette exercice:
Calculer les limite suivantes :
1) lim x->0 [(racine carré 1+x)-1] au carrée le tout divisée par xsinx
2) lim x->0 epx^x-(racine carré 1+x) le tout divisée par x
3) lim x->+ infini sinx/lnx

Je vous remercie

Qu'as-tu essayé?

Pour t'aider à démarrer, pour la première question, tu multiplies le numérateur et le dénominateur par

[Nedroma]

Qu'as-tu essayé?

Pour t'aider à démarrer, pour la première question, tu multiplies le numérateur et le dénominateur par

Oui c'est ce que j'ai fais je sais juste qu'il faut toujours multiplier en haut et en bas par le conjugué

[mrif]

Oui c'est ce que j'ai fais je sais juste qu'il faut toujours multiplier en haut et en bas par le conjugué

Et qu'est ce que tu as trouvé?

[mathelot]

soit
on peut également écrire

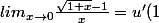[mrif]

soit
on peut également écrire

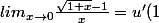C'est bien vu mais ça ne marche pas car le 2 ème facteur n'a pas de limite en 0.

[mathelot]

on étudie

[chan79]

on étudie

oui, ou alors les DL

[mrif]

on étudie

Là ça marche, mais je pense qu'il est plus simple d'opter pour la méthode utilisant les conjugués.

[Nedroma]

Là ça marche, mais je pense qu'il est plus simple d'opter pour la méthode utilisant les conjugués.

Je vous remerci pour votre aide

[aymanemaysae]

Pour lim(x-->0) {(exp(x)-rcarée(1+x))/x} = lim(x-->0) {(exp(x) -1)/x} - lim(x-->0) {(rcarée(1+x)-1)/x}
= exp(0) - 1/(2rcarrée(1+0)) = 1 - 1/2 = 1/2 .

[aymanemaysae]

Et pour lim (x--> +infini) {sin(x)/Ln(x)}, on a d'abord Ln(x) > 0 pour x très grand, et comme -1 <= sin(x) <= 1, donc
-1/Ln(x) <= sin(x)/Ln(x) <= 1/Ln(x) , donc vabolue(sin(x)/Ln(x)) <= 1/Ln(x) pour x très grand.
On a aussi lim (x--> +infini) {1/Ln(x)} = 0 , donc lim (x--> +infini) {sin(x)/Ln(x)} = 0 .