DM Suites arithmétiques
14 messages
- Page 1 sur 1
DM Suites arithmétiques
Bonjour,
Je bloque sur un exercice de mon devoir de maths de première sur deux exercices, je vous remercie.
Tout d'abord dans cette partie on nous donne l'expression de u(n)= 1/(2n+1), puis:
on nous demande d'étudier le sens de variation de u(n), alors j'ai fait la différence de u(n+1)-u(n) et jai trouvé un produit négatif mais je ne suis pas sur de mon résultat.
Ensuite on nous demande de conjecturer la limite de u(n), là je bloque :mur: je pensais résoudre une inéquation avec
0>un+1-un
Merci votre aide, cordialement.
Je bloque sur un exercice de mon devoir de maths de première sur deux exercices, je vous remercie.
Tout d'abord dans cette partie on nous donne l'expression de u(n)= 1/(2n+1), puis:
on nous demande d'étudier le sens de variation de u(n), alors j'ai fait la différence de u(n+1)-u(n) et jai trouvé un produit négatif mais je ne suis pas sur de mon résultat.
Ensuite on nous demande de conjecturer la limite de u(n), là je bloque :mur: je pensais résoudre une inéquation avec
0>un+1-un
Merci votre aide, cordialement.
Ineedyourhelp a écrit:Bonjour,
Je bloque sur un exercice de mon devoir de maths de première sur deux exercices, je vous remercie.
Tout d'abord dans cette partie on nous donne l'expression de u(n)= 1/(2n+1), puis:
on nous demande d'étudier le sens de variation de u(n), alors j'ai fait la différence de u(n+1)-u(n) et jai trouvé un produit négatif mais je ne suis pas sur de mon résultat.
Ensuite on nous demande de conjecturer la limite de u(n), là je bloque :mur: je pensais résoudre une inéquation avec
0>un+1-un
Merci votre aide, cordialement.
Conclusion ...
Salut,
Quand on a expression de la suite sous la forme , on peut simplement étudier son sens de variation comme une fonction classique, ça revenait peut-être un peu plus simple que faire la différence de
, on peut simplement étudier son sens de variation comme une fonction classique, ça revenait peut-être un peu plus simple que faire la différence de 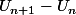 , je ne sais pas...
, je ne sais pas...
Sinon, pour la deux, c'est normal que tu n'aies jamais vu : Ce n'est pas pour rien qu'on demande de conjecturer et non de démontrer.
Quand on demande de conjecturer, il ne faut pas se casser la tete : Simplement donner la réponse qui semble la plus évidente, la plus logique, il n'y a pas de justification à donner.
En l'occurrence, tu peux conjecturer la limite comme le suggère Carpate ( même si tu verras plus tard, la limite ne sera pas forcément celle ci ).
Quand on a expression de la suite sous la forme
Sinon, pour la deux, c'est normal que tu n'aies jamais vu : Ce n'est pas pour rien qu'on demande de conjecturer et non de démontrer.
Quand on demande de conjecturer, il ne faut pas se casser la tete : Simplement donner la réponse qui semble la plus évidente, la plus logique, il n'y a pas de justification à donner.
En l'occurrence, tu peux conjecturer la limite comme le suggère Carpate ( même si tu verras plus tard, la limite ne sera pas forcément celle ci ).
Grimmys a écrit:Salut,
Quand on a expression de la suite sous la forme, on peut simplement étudier son sens de variation comme une fonction classique, ça revenait peut-être un peu plus simple que faire la différence de
, je ne sais pas...
Sinon, pour la deux, c'est normal que tu n'aies jamais vu : Ce n'est pas pour rien qu'on demande de conjecturer et non de démontrer.
Quand on demande de conjecturer, il ne faut pas se casser la tete : Simplement donner la réponse qui semble la plus évidente, la plus logique, il n'y a pas de justification à donner.
En l'occurrence, tu peux conjecturer la limite comme le suggère Carpate ( même si tu verras plus tard, la limite ne sera pas forcément celle ci ).
Merci de ta réponse, tu m'éclaire néanmoins' je ne comprends toujours pas car le therme de limite ne me dit rien.
Ineedyourhelp a écrit:Merci de ta réponse, tu m'éclaire néanmoins' je ne comprends toujours pas car le therme de limite ne me dit rien.
Bonjour,
parce que tout simplement, les limites ne sont pas au programme de première S mais dit autrement:
On cherche vers quoi se "rapprochent" les termes de la suite (un) quand n devient de "plus en plus grand" (quand n->+oo)
Ineedyourhelp a écrit:D'après ce que vous m'avez dit je peux juste conclure par u(n) tend vers moins l'infini ?
(re) bonjour,
non, mais comme dit avant on demande juste de conjecturer autrement dit que peut-on constater sans le démontrer.
On peut calculer quelques termes de la suite pour des valeurs de n très grande et "regarder" ce qui se passe.
Sinon, pour aller plus loin, on peut essayer de décomposer pour arriver à savoir ce qui se passe pour Un quand n devient très grand.
Par exemple quand n->+oo (n devient infiniment grand)
que se passe-t-il pour 2n+1?
puis pour 1/(2n+1)?
Ah oui pardon, j'avais pas vu que tu étais en première... J'ai pensé bêtement que tu étais élève de terminal ayant déjà eu une première approche des limites...
Ça m'étonne vraiment qu'on te donne cette exercice alors... Car qui plus est, la notion de suite minorée / majorée tu n'as pas vu non plus ?
Bref, pour en revenir à ton problème, non, ta réponse est fausse : Dire que la limite de ta fonction est - infini revient à dire que pour n de plus en plus grand, les valeurs sont de plus en plus petite vers - infini.
Cad qu'on obtiendrait par exemple U1000 = - 44783628 et U1500 = - 7852045, tu saisis ?
Ta suite semblerait-elle pas plus se rapprocher vers une valeur fixe plutôt que des valeurs infiniment petites / grandes ?
Ça m'étonne vraiment qu'on te donne cette exercice alors... Car qui plus est, la notion de suite minorée / majorée tu n'as pas vu non plus ?
Bref, pour en revenir à ton problème, non, ta réponse est fausse : Dire que la limite de ta fonction est - infini revient à dire que pour n de plus en plus grand, les valeurs sont de plus en plus petite vers - infini.
Cad qu'on obtiendrait par exemple U1000 = - 44783628 et U1500 = - 7852045, tu saisis ?
Ta suite semblerait-elle pas plus se rapprocher vers une valeur fixe plutôt que des valeurs infiniment petites / grandes ?
Grimmys a écrit:Ah oui pardon, j'avais pas vu que tu étais en première... J'ai pensé bêtement que tu étais élève de terminal ayant déjà eu une première approche des limites...
Ça m'étonne vraiment qu'on te donne cette exercice alors... Car qui plus est, la notion de suite minorée / majorée tu n'as pas vu non plus ?
Bref, pour en revenir à ton problème, non, ta réponse est fausse : Dire que la limite de ta fonction est - infini revient à dire que pour n de plus en plus grand, les valeurs sont de plus en plus petite vers - infini.
Cad qu'on obtiendrait par exemple U1000 = - 44783628 et U1500 = - 7852045, tu saisis ?
Ta suite semblerait-elle pas plus se rapprocher vers une valeur fixe plutôt que des valeurs infiniment petites / grandes ?
Merci, en fait je pense que pour n plus grand la valeur de u (n) tend verd 0,001
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
