Un exercie d'analyse

[Bahana98]

Salut, svp Soit f une fct numérique définie sur [0,1] telle que f(1)<0<f(0) et g une fct numérique continue sur [0,1]. supposons que f+g croissante. Montrer qu'il existe c appartient à [0,1] tel que f(c)=0.
Merci d'avance pour votre indications.

[capitaine nuggets]

Salut !

Si n'est pas continue je ne pense pas que ce soit vrai ; je ne vois pas l'intérêt de parler de 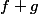si ne sert à rien...

[Bahana98]

f n'est pas forcément continue, en effet prenons g la fonction nulle est continue et f+g=f croissante n'implique plus que f est continue(la croissance n'implique pas la continuité)

[capitaine nuggets]

Salut, svp Soit f une fct numérique définie sur [0,1] telle que f(1)<0<f(0) et g une fct numérique continue sur [0,1]. supposons que f+g croissante. Montrer qu'il existe c appartient à [0,1] tel que f(c)=0.
Merci d'avance pour votre indications.

Ne voulais-tu pas dire (f+g)(c)=0 ?

[Bahana98]

nn, c'est f(c)=0

[MouLou]

salut. Je crois que j ai une idée. On a par croissance de f+g et par hypothese sur f(0) et f(1)
g(0)<f+g(0)<=f+g(1)<g(1). Donc en gros il y a un moment ou f+g va passer en dessous de g. Pour ça on considère A={x,g(x)<=f+g(x)}. On prend sup. de A=x0. Et l hypothèse f+g croissante permet d avoir une limite à gauche et à droite pour f+g en x0. En travaillant encore un peu on peut arriver a f(x0)=0 je pense!

[Bahana98]

il existe une suite xn de A qui tend vers x0,or xn=0, il reste à montrer que f(x0)<=0.

[Bahana98]

c'est une bonne idée , mais j'ai pas encore montrer ce qui reste , je bloque

[MouLou]

Puisque f+g a une limite à gauche et à droite en x0 et que g est continue, on en déduit que f a une limite à gauche et à droite en x0.

Par ailleurs lim en x0 par valeurs inférieures de f+g est supérieure à g(x0), tandis que lim par valeur supérieure est inférieure à g(x0).

En écrivant les limites, on a f(x0-)>=0, f(x0+)<=0.

La on utilise une dernière hypothèse: la croissance de f+g qui donne f(x0-)<=f(x0+). De la c est terminé.

[Bahana98]

pourquoi lim(f+g)(x) x0+

[MouLou]

car pour tout en d'autres termes, pour tout

[Bahana98]

Merci infiniment.