Meme avec la réponse je ne comprend pas

[DV4 Samy]

Bonjour et merci de m'avoir accepter sur ce groupe. Actuellement en terminale S j'aimerais comprendre la signification de (l2 – l – 0,24) = 0. Ecrit "simplement" ça donne quoi svp ^^

[chan79]

Bonjour et merci de m'avoir accepter sur ce groupe. Actuellement en terminale S j'aimerais comprendre la signification de (l2 – l – 0,24) = 0. Ecrit "simplement" ça donne quoi svp ^^

salut
une équation du second degré ??????
i²-i-0,24=0

delta=1,4²

[Laurent Watteau]

Je note que 0.24 est le 100ème de 24.
En y regardant d'un peu plus près je constate que 24 est une permutation des chiffres du nombre 42 qui est ... le nombre le plus important à connaitre

Pour moi c'est une piste à explorer...

Blague à part, c'est difficile de donner un sens précis à cette question, non ?

[DV4 Samy]

Rebonjour et désolé pour hier
Je ne sais pas dans l'exo je dois avec
Ensemble E n-1-xn=0.24xn-1
avec t(n)=lambda^n
Démontrer que la suite appartient a E et a pour soluce lambda^2-lambda-0.24=0
Ma prof ma envoyé "avec ça tu peux comprendre (l2 – l – 0,24) = 0." Mais je ne comprend pas comment l'utiliser en gros

[Laurent Watteau]

Notes préliminaires :

• Attention, je suppose qu'il y a une erreur dans ce que tu viens d'écrire :
  Il doit probablement s'agir de et non
• Tu ne le précises pas mais je supposerai ci-dessous que (vérifie l'énoncé exact).

Ma proposition :
On appelle donc l'ensemble des suites qui vérifient la relation .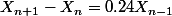

Ce que l'on veut trouver, ce sont les conditions sur pour que la suite définie par 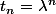soit un élément de E (c'est à dire les conditions pour qu'une telle suite vérifie la relation ci-dessus).

Tu dois par conséquent avoir .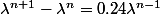
Tu passes tous les termes du même côté de l'équation puis tu factorises par ; tu obtiens alors

Un produit de facteur est nul ssi un de ses facteurs est nul. Or puisque .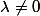

On doit donc fatalement avoir .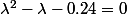
C.Q.F.D.

Bien sûr ensuite je te laisse continuer... Tu chercheras les racines de cette équation du second degré, tu en déduiras toute une famille(*) de suites satisfaisant la relation.

A+
Laurent.

(*) Suggestion : Supposons que et soient deux suites vérifiant la propriété de l'énoncé. Que penserais-tu d'une suite définie par 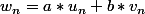, et étant deux réels quelconques ?

[DV4 Samy]

Bonjour
1000 merci à toi ^^ j'ai enfin compris

[DV4 Samy]

Merci aussi ^^ je n'avais pas vu ton message (je ne suis pas un habitué du site =) )