Bonjour j'ai 2 démos à faire besoin d'aide svp
Pour le cas d'indépendance, V(aX + bY) = a²V(X) + b²V(Y)
et
Cov (aX + bX+Y)= a b V(X)
Pour la première je trouve :
V(aX + bY) = E(aX + bY)² - [E(aX + bY)]² = E(a²X² + 2abXY + b²Y²) - [aE(X) + bE(Y)]²
= a²E(X²) + 2abE(XY) + b²E(Y²) - a²[E(X)]² - 2abE(X)E(Y) - b²[E(Y)]²
= a²[E(X²) - (E(X))²] + b²[E(Y²) - (E(Y))²] + 2ab[E(XY) - E(X)E(Y)]
= a²V(X) + b²V(Y) + 2ab[E(XY) - E(X)E(Y)]
mais ce n'est pas le résultat attendu
:help:
Statistiques démo de V(aX + bY) = a²V(X) + b²V(Y)
8 messages
- Page 1 sur 1
Alors tu peux appliquer ce résultat ici, puisqu'il figure dans ton cours.
Un membre du forum, sans doute trop timide pour poster, fait part par message privé du fait qu'il n'arrive pas à démontrer que la covariance-E(X)E(Y)) de deux variables aléatoires indépendantes est nulle.
de deux variables aléatoires indépendantes est nulle.
Pour faire simple, supposons que (resp.
(resp.  ) prend ses valeurs dans une partie finie
) prend ses valeurs dans une partie finie  (resp.
(resp.  ) de
) de  . L'indépendance de
. L'indépendance de  et
et  signifie que pour tout
signifie que pour tout ) dans
dans  ,
,
 =P(X=i)\times P(Y=j))
(autrement dit, si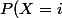\neq 0) , la probabilité que
, la probabilité que 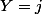 sachant que
sachant que 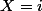 est égale à la probabilité de
est égale à la probabilité de 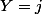 : la valeur prise par
: la valeur prise par  est indépendante de celle prise par
est indépendante de celle prise par  (et vice-versa)).
(et vice-versa)).
Alors, si et
et  sont indépendantes :
sont indépendantes :
=\sum_{(i,j)\in I\times J} ij\,P(X=i \text{ et } Y=j)= \sum_{(i,j)\in I\times J}( i\,P(X=i))\,(j\,P(Y=j))= \left(\sum_{i\in I} i\,P(X=i)\right)\left(\sum_{j\in J} j\,P(Y=j)\right)=E(X)\,E(Y)\;.)
Un membre du forum, sans doute trop timide pour poster, fait part par message privé du fait qu'il n'arrive pas à démontrer que la covariance
Pour faire simple, supposons que
(autrement dit, si
Alors, si
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
