Bonjour,
Comment montre t'on qu'une matrice est définie positive ?
Matrice définie positie
11 messages
- Page 1 sur 1
Ca dépend comment cette matrice arrive. Il y a plusieurs moyens possibles : voir que la matrice s'écrit 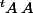 avec
avec  carrée inversible, montrer que les mineurs principaux sont tous >0, s'apercevoir que les valeurs propres sont toutes >0, décomposer la forme quadratique associée en carrés par l'algorithme de Gauss, etc.
carrée inversible, montrer que les mineurs principaux sont tous >0, s'apercevoir que les valeurs propres sont toutes >0, décomposer la forme quadratique associée en carrés par l'algorithme de Gauss, etc.
...
Ma matrice s'écrit
M =
1 2 3
2 5 1
3 1 35
le but est de faire une factorisation de Cholesky (méthode que j'ai comprise)
Mais pour déterminer si la décomposition de Cholesky est applicable il faut montrer qu'elle est symétrique définie positive
Pour montrer qu'elle est symétrique on montre que tM = M
Pour montrer que la matrice est définie positive mon professeur montre que . X
avec X =
x1
x2
x3
est strictement positive pour tout X de R^3
cette méthode semble plus fastidieuse que celles que vous avez énoncé notamment celle des mineurs principaux alors pourquoi mon professeur s'encombre t'il de cette méthode. De quelle façon procéderiez vous ?
Merci
M =
1 2 3
2 5 1
3 1 35
le but est de faire une factorisation de Cholesky (méthode que j'ai comprise)
Mais pour déterminer si la décomposition de Cholesky est applicable il faut montrer qu'elle est symétrique définie positive
Pour montrer qu'elle est symétrique on montre que tM = M
Pour montrer que la matrice est définie positive mon professeur montre que . X
avec X =
x1
x2
x3
est strictement positive pour tout X de R^3
cette méthode semble plus fastidieuse que celles que vous avez énoncé notamment celle des mineurs principaux alors pourquoi mon professeur s'encombre t'il de cette méthode. De quelle façon procéderiez vous ?
Merci
Petit détail : strictement positive pour tout X différent de 0
Si le but est d'arriver à une factorisation de Cholesky, l'algorithme de décomposition en carrés me semble tout indiqué, puisqu'en même temps qu'on prouve que la matrice est définie positive, on récupère une factorisation. D'après ce que je comprends, c'est ce que fait ton prof ?
J'ajoute que la décomposition de Gauss se fait ici en deux coups de cuillère à pot. Les coefficients sont choisis pour que tout se passe bien.
Si le but est d'arriver à une factorisation de Cholesky, l'algorithme de décomposition en carrés me semble tout indiqué, puisqu'en même temps qu'on prouve que la matrice est définie positive, on récupère une factorisation. D'après ce que je comprends, c'est ce que fait ton prof ?
J'ajoute que la décomposition de Gauss se fait ici en deux coups de cuillère à pot. Les coefficients sont choisis pour que tout se passe bien.
Oui c'est bien cela on obtient un long développement avec des x1^2, x2^2, x3^2, x1x2, x2x3, x1x3 et ensuite on factorise pour prouver le fait que l'expression est positive pour tout X différent de zéro mais cela me fait peur car il n'existe pas de méthode pré-définie pour factoriser une telle expression c'est un peu "instinctif" ?
Emma.S a écrit:Oui c'est bien cela on obtient un long développement avec des x1^2, x2^2, x3^2, x1x2, x2x3, x1x3 et ensuite on factorise pour prouver le fait que l'expression est positive pour tout X différent de zéro mais cela me fait peur car il n'existe pas de méthode pré-définie pour factoriser une telle expression c'est un peu "instinctif" ?
Pas si long que ça, et il y a un algorithme pour décomposer en carrés (et non pas pour factoriser !) : l'algorithme de Gauss, que tu trouveras dans tout bon manuel (ou par exemple ici, même si ce n'est pas ce qu'on fait de mieux.
La décomposition en carrés n'est pas une factorisation de l'expression (la forme quadratique) en  . Tu ne le vois pas ?
. Tu ne le vois pas ?
Je fais l'exemple (avec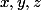 plutôt que
plutôt que 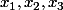 ) :
) :
= x^2+4xy+6xz+ 5y^2+ 2yz+ 35 z^2)
On complète le carré à partir de de façon à ne plus avoir de
de façon à ne plus avoir de  dans ce qui reste :
dans ce qui reste :
=(x+2y+3z)^2 -(4y^2+12yz+9z^2)+ 5y^2+ 2yz+ 35 z^2=(x+2y+3z)^2+y^2-10yz+26z^2)
On complète le carré à partir de de façon à ne plus avoir de
de façon à ne plus avoir de  dans ce qui reste :
dans ce qui reste :
=(x+2y+3z)^2+(y-5z)^2-25z^2+26z^2=(x+2y+3z)^2+(y-5z)^2+z^2)
On n'a pas factorisé !
!
Je fais l'exemple (avec
On complète le carré à partir de
On complète le carré à partir de
On n'a pas factorisé
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
