Bonus pour interrogation !

[Vahiné Piquante]

Bonsoir, bonsoir !

Mon petit frère a récemment eu droit à une interrogation surprise à cause de deux de ses camarades qui bavardaient. N'étant pas très fort en maths, il a eu une très mauvaise note. Il est très déçu de commencer l'année sur cette mauvaise note. Le professeur - pas si méchant que ça finalement - leur a laissé la chance de se rattraper en leur promettant 6 points bonus. La condition étant de résoudre cette équation. Moi même étant dans le supérieur n'est pu la résoudre. Peut-être que je me complique trop la vie alors que c'est évident. Je suis plutôt aisée dans cette matière mais cela m'attriste de ne pouvoir aider mon frère ! Pourriez-vous à votre tour essayer de l'aider ? C'est pour une bonne cause ! Merci d'avance aux personnes qui répondront. (:

Résoudre l'ensemble des entiers naturels :
11 + a^2b^3c^2 + a^2b^2c + a = 1993

[chan79]

Bonsoir, bonsoir !

Mon petit frère a récemment eu droit à une interrogation surprise à cause de deux de ses camarades qui bavardaient. N'étant pas très fort en maths, il a eu une très mauvaise note. Il est très déçu de commencer l'année sur cette mauvaise note. Le professeur - pas si méchant que ça finalement - leur a laissé la chance de se rattraper en leur promettant 6 points bonus. La condition étant de résoudre cette équation. Moi même étant dans le supérieur n'est pu la résoudre. Peut-être que je me complique trop la vie alors que c'est évident. Je suis plutôt aisée dans cette matière mais cela m'attriste de ne pouvoir aider mon frère ! Pourriez-vous à votre tour essayer de l'aider ? C'est pour une bonne cause ! Merci d'avance aux personnes qui répondront. (:

Résoudre l'ensemble des entiers naturels :
11 + a^2b^3c^2 + a^2b^2c + a = 1993

salut
Si l'énoncé est bien 11+a²b³c²+a²b²c+a=1993
ça donne:
a²b³c²+a²b²c+a=1982
Factoriser a et décomposer 1982

[capitaine nuggets]

Salut !

Je ne l'ai pas résolue mais je pense qu'en l'écrivant sous la forme , on commence à avoir quelque chose.

Or se décompose en facteurs premiers sous la forme .

Donc de , cela revient à résoudre les deux systèmes :

deux systèmes :

1) et ;
2) et .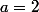

En cherchant à factoriser comme je l'ai fait au début, raisonne de manière analogue pour trouver b et c.

:+++:

[cyrill]

Bonsoir, bonsoir !

Mon petit frère a récemment eu droit à une interrogation surprise à cause de deux de ses camarades qui bavardaient. N'étant pas très fort en maths, il a eu une très mauvaise note. Il est très déçu de commencer l'année sur cette mauvaise note. Le professeur - pas si méchant que ça finalement - leur a laissé la chance de se rattraper en leur promettant 6 points bonus. La condition étant de résoudre cette équation. Moi même étant dans le supérieur n'est pu la résoudre. Peut-être que je me complique trop la vie alors que c'est évident. Je suis plutôt aisée dans cette matière mais cela m'attriste de ne pouvoir aider mon frère ! Pourriez-vous à votre tour essayer de l'aider ? C'est pour une bonne cause ! Merci d'avance aux personnes qui répondront. (:

Résoudre l'ensemble des entiers naturels :
11 + a^2b^3c^2 + a^2b^2c + a = 1993

Est-on certain qu'il y ait une solution ?
si on met 11 de l'autre côté on arrive à
a^2b^3c^2 + a^2b^2c + a = 1982 = 2(991)
d'où a( ab^3c^2 + ab^2c + 1)= 2(991)
il me semble que ça doit impliquer a = 2 et ab^3c^2 + ab^2c + 1 =991

donc 2b^3c^2 + 2b^2c = 990 puis b^3c^2 + b^2c = 495
495 = 3^2*5*11 et b^3c^2 + b^2c = b^2*c*(bc+1) donc b= 3 mais alors
c(3c+1)= 5*11 ? c= 5 ou 11 mais ça ne marche pas
ou bien b = 1 mais alors c(c+1)= 495 ne convient pas non plus ...
je ne vois plus quoi essayer

[mathelot]

Est-on certain qu'il y ait une solution ?

b=0 donne une solution

[cyrill]

b=0 donne une solution

oui c'est vrai , a= 1982 b=0 ( ou c =0) ; espérons qu'ils auront tous le bonus !

[WillyCagnes]

dans le cas où il s'est trompé dans l'énoncé comme 1992 au lieu de 1993
11 + a^2b^3c^2 + a^2b^2c + a = 1992

a=b=1
c=44

[Vahiné Piquante]

Ouah, je ne m'attendais pas à avoir autant de réponses. Merci à vous !
WillyCagnes, tu m'a fait constater qu'il y avait bien une erreur dans l'énoncé. Pas là où tu pensais mais au deuxième membre. Mon petit frère a mal recopié son énoncé. Rho ~
Donc bon, je suis sincèrement désolée.

L'énoncé - le vrai cette fois - est : 11+ a^3b^3c^2 + a^2b^2c + a = 1993.

Mes sincères excuses.

Par ailleurs, j'avais moi-même essayer de factoriser, en vain. Cela ne mène à rien. Enfin, je crois.
Le problème est que l'on ait trois inconnus dans une seule et même équation !

Oui, espérons qu'ils aient tous le bonus Cyrill. La meilleure note ne dépasse pas les 8 sur 20...