[1ère] Relation d'ordre dans R
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
NeoNeo
- Messages: 5
- Enregistré le: 08 Juin 2014, 20:52
-
 par NeoNeo » 10 Sep 2015, 13:54
par NeoNeo » 10 Sep 2015, 13:54
Bonjour

Aujourd'hui le prof a entamé une nouvelle matière, la relation d'ordre dans R
http://www.noelshack.com/2015-37-1441889291-iphone-image-09-10-2015.jpghttp://www.noelshack.com/2015-37-1441889331-iphone-image-09-10-2015.jpg( je suis désolé d'avoir recours à un hébergeur d'image mais sur mobile, mon téléphone crashe lorsque j'utilise la fonction "joindre une photo" )
En fait je ne comprends pas trop comment se fait-il que dans le point 1, x peut être plus petit ou égal à x
Donc si je me sers d'un exemple, 2 peut être plus petit ou égal à lui même ??
Et quand bien même il serait petit, x-x=0ER- au lieu de R+ ?
Et enfin je ne comprends pas trop cette notion "d'ordre total"dans le point 2
J'aimerais avoir de plus amples explications pour pouvoir établir les propriétés supplémentaires du point 3 moi même ( pour mercredi prochain )
Merci beaucoup

-
mathelot
 par mathelot » 10 Sep 2015, 14:09
par mathelot » 10 Sep 2015, 14:09
NeoNeo a écrit:Bonjour

Aujourd'hui le prof a entamé une nouvelle matière, la relation d'ordre dans R
http://www.noelshack.com/2015-37-1441889291-iphone-image-09-10-2015.jpghttp://www.noelshack.com/2015-37-1441889331-iphone-image-09-10-2015.jpg( je suis désolé d'avoir recours à un hébergeur d'image mais sur mobile, mon téléphone crashe lorsque j'utilise la fonction "joindre une photo" )
En fait je ne comprends pas trop comment se fait-il que dans le point 1, x peut être plus petit ou égal à x
Donc si je me sers d'un exemple, 2 peut être plus petit ou égal à lui même ??
Et quand bien même il serait petit, x-x=0ER- au lieu de R+ ?
Et enfin je ne comprends pas trop cette notion "d'ordre total"dans le point 2
J'aimerais avoir de plus amples explications pour pouvoir établir les propriétés supplémentaires du point 3 moi même ( pour mercredi prochain )
Merci beaucoup

une propriété "A ou B" est vérifiée si A vraie ou B est vraie.
donc x est inférieur ou égal à lui même car x=x
pour l'ordre total, faire par disjonction des cas


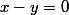
-
NeoNeo
- Messages: 5
- Enregistré le: 08 Juin 2014, 20:52
-
 par NeoNeo » 10 Sep 2015, 15:19
par NeoNeo » 10 Sep 2015, 15:19
mathelot a écrit:une propriété "A ou B" est vérifiée si A vraie ou B est vraie.
donc x est inférieur ou égal à lui même car x=x
pour l'ordre total, faire par disjonction des cas


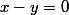
Merci beaucoup, mais je ne comprends le "est un diviseur" que le prof a mît au tableau
-
mathelot
 par mathelot » 10 Sep 2015, 15:26
par mathelot » 10 Sep 2015, 15:26
NeoNeo a écrit:Merci beaucoup, mais je ne comprends le "est un diviseur" que le prof a mît au tableau
a|b (a divise b) est une relation d'ordre non total sur N*
-
NeoNeo
- Messages: 5
- Enregistré le: 08 Juin 2014, 20:52
-
 par NeoNeo » 10 Sep 2015, 22:02
par NeoNeo » 10 Sep 2015, 22:02
Merci énormément j'ai enfin compris


-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 10 Sep 2015, 22:10
par Sake » 10 Sep 2015, 22:10
Il est extrêmement surprenant (et plutôt satisfaisant) de voir que les classes de 1ère S reviennent aux fondamentaux de l'algèbre d'une façon si peu communément rigoureuse !

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Sep 2015, 22:24
par zygomatique » 10 Sep 2015, 22:24
Sake a écrit:Il est extrêmement surprenant (et plutôt satisfaisant) de voir que les classes de 1ère S reviennent aux fondamentaux de l'algèbre d'une façon si peu communément rigoureuse !
ce n'est surement pas dans l'enseignement français ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
NeoNeo
- Messages: 5
- Enregistré le: 08 Juin 2014, 20:52
-
 par NeoNeo » 06 Oct 2015, 17:24
par NeoNeo » 06 Oct 2015, 17:24
zygomatique a écrit:ce n'est surement pas dans l'enseignement français ...
Oui c'est juste, c'est l'enseignement belge

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
