Equation differentielle 2em d avec 2nd membre

[Natsu24950]

Bonjour voila le blem:
Donner l'expression de la solution general (equ sans sd mbre) sachant que (equ. caracteristique admet un discriminant negatif.) en fonction de 2 solution particuliers(ça c'est facile )
puis montrer que cette solution peut se mettre sous la fomre
y_g=e^;)x (A cos;);)x+B sin;);)x )
merci d'avance

[Robot]

Indice : et sont les deux solutions conjuguées de l'équation caractéristique.

[Natsu24950]

Indice : et sont les deux solutions conjuguées de l'équation caractéristique.

Oui je sais ça mais après pour la linéarisation et la transformation à la forme demandée je n'ai pas su, on m'a dit que c'est une tout autre méthode, mais je la connais pas

[paquito]

Tu dois donc savoir que quelques soient les complexes et, décrit l'espace vectoriel de dimension 2 sur C des solutions de l'équation homogène.

Mais en faisant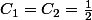, tu obtiens

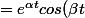Et en faisant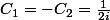 , tu obtiens

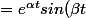Tu as donc deux solutions réelles et linéairement indépendantes qui forment donc une base de l'espace vectoriel sur R de dimension 2 des solutions réelles de l équation homogène et leur écriture avec cos et sin.

[mathelot]

est ce que l'ensemble des solutions complexes ( K=C)
est le complexifié de l'e.v des solutions réelles (K=R) ?

[Robot]

Vu que l'espace vectoriel des solutions est de dimension 2 (que ce soit sur R pour les solutions réelles ou sur C pour les solutions complexes)