Bonjour,
J'ai un partiel en fin de semaine prochaine sous forme de QCM. Lorsque je fais des entraînements je tombe parfois sur des questions du style "Le DL3(2) de x^2 est:" ou encore "Le DL3(2) de
x^3 est:"
D'après les corrections, la réponse à la première question est :4+4(x-2)+(x-2)^2+(1/6)(x-2)^3+reste et de la deuxième question est: 8+12(x-2)+6(x-2)^2+(x-2)^3+reste
mais j'aimerai bien comprendre comment en arrive-t-on à ces résultats.
En faisant la formule de Taylor-Young je n'obtiens rien de cette forme et aucune formule dite "usuelle" ne permet une étude de ces fonctions.
Si vous avez des pistes je suis toute ouïe.:zen:
Merci d'avance,
Ps: Quel est lintérêt du DL sur ces fonctions? Il semble plus difficile à calculer que la fonction en elle même.
Développements limités
4 messages
- Page 1 sur 1
Bonjour,
Pour le DL de x^n en a il suffit normalement d'écrire x^n = (x-a+a)^n et d'utiliser la formule du binôme.
La correction du DL de x^2 en 2 est fausse manifestement : il ne peut pas y avoir de terme d'ordre 3 (on obtient en fait une égalité plutôt qu'une approximation, en gros le o(...) va être nul).
Et ça peut être utile par exemple pour des études locales de tes polynômes (maxima, minimas, points d'inflexions, etc...) même si ça reste en effet des choses très simples.
Pour le DL de x^n en a il suffit normalement d'écrire x^n = (x-a+a)^n et d'utiliser la formule du binôme.
La correction du DL de x^2 en 2 est fausse manifestement : il ne peut pas y avoir de terme d'ordre 3 (on obtient en fait une égalité plutôt qu'une approximation, en gros le o(...) va être nul).
Et ça peut être utile par exemple pour des études locales de tes polynômes (maxima, minimas, points d'inflexions, etc...) même si ça reste en effet des choses très simples.
Et pourtant...
dans les deux cas, il y a des tas de méthodes, dont évidement la formule de Taylors-Young et une/des "formule dite usuelle".
1) Taylors-Young : (pas malin ici, mais on peut)
=f(x_o)+f'(x_o)(x-x_o)+\frac{f''(x_o)}{2!}(x-x_o)^2+\frac{f'''(x_o)}{3!}(x-x_o)^3+...)
Si=x^2) et
et 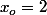 alors
alors =4\ ;\ f'(x_o)=2x_o=4\ ;\ f''(x_o)=2) et les dérivées suivantes sont nulles donc
et les dérivées suivantes sont nulles donc
=4+4(x-2)+(x-2)^2)
2) Formule usuelle : (encore moins malin ici, mais on peut)
Si on pose (Le truc à faire systématiquement pour utiliser les "formules usuelles" vu qu'elle sont toutes en
(Le truc à faire systématiquement pour utiliser les "formules usuelles" vu qu'elle sont toutes en  ) alors
) alors
=x^2=(2+h)^2=2^2\big(1+\frac{h}{2}\big)^2)
Or (formule usuelle) pour on a
on a ^\alpha=1+\alpha t+\frac{\alpha(\alpha-1)}{2!}t^2++\frac{\alpha(\alpha-1)(\alpha-2)}{3!}t^2+)
que l'on applique bêtement avec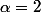 et
et 
3) Méthode intelligente dans un cas pareil :
Celle donnée par L.A.
Sinon, intérêt du bidule :
- Dans un cas comme celui proposé par l'exercice où la fonction est un polynôme, quasi aucun intérêt : on s'en sort très bien sans les D.L.
- Dans les cas intéressant où la fonction n'est pas un polynômes, des tonnes d'applications : calculs de limites, d'asymptotes, de position de la courbe par rapport aux asymptotes, recherche d'équivalent simple de la fonction, etc etc etc
En fait, tout ce qui concerne l'étude locale de la fonction peut (doit ?) se faire à l'aide de D.L.
dans les deux cas, il y a des tas de méthodes, dont évidement la formule de Taylors-Young et une/des "formule dite usuelle".
1) Taylors-Young : (pas malin ici, mais on peut)
Si
2) Formule usuelle : (encore moins malin ici, mais on peut)
Si on pose
Or (formule usuelle) pour
que l'on applique bêtement avec
3) Méthode intelligente dans un cas pareil :
Celle donnée par L.A.
Sinon, intérêt du bidule :
- Dans un cas comme celui proposé par l'exercice où la fonction est un polynôme, quasi aucun intérêt : on s'en sort très bien sans les D.L.
- Dans les cas intéressant où la fonction n'est pas un polynômes, des tonnes d'applications : calculs de limites, d'asymptotes, de position de la courbe par rapport aux asymptotes, recherche d'équivalent simple de la fonction, etc etc etc
En fait, tout ce qui concerne l'étude locale de la fonction peut (doit ?) se faire à l'aide de D.L.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
