Calcul d'une primitive
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
vanyle
- Messages: 4
- Enregistré le: 10 Mar 2015, 20:07
-
 par vanyle » 19 Avr 2015, 13:01
par vanyle » 19 Avr 2015, 13:01
Bonjour à tous :happy2:
J'ai besoin d'aide pour un calcul dans la question suivante :
Montrer que la fonction G définie sur ]0;+

[ par G(x) =
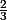


est une primitive de la fonction g définie sur le même intervalle par g(x) =
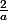

où a=e d'après une question précédente
Je cherche à montrer que G'(x) = g(x) :
G'(x) =
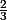

+

G'(x) =

+

G'(x) =

+

G'(x) =

G'(x) =

G'(x) =

alors que g(x) =
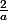

où a=e d'après une question précédente
Comment faire ?
Merci de votre aide

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 19 Avr 2015, 13:11
par WillyCagnes » 19 Avr 2015, 13:11
Bonjour
G(x) =
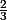
.

la derivée est
G'(x) =

-
vanyle
- Messages: 4
- Enregistré le: 10 Mar 2015, 20:07
-
 par vanyle » 19 Avr 2015, 13:15
par vanyle » 19 Avr 2015, 13:15
WillyCagnes a écrit:Bonjour
G(x) =
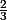
x

la derivée est
G'(x) =

Pardon..c'est G(x) =
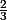


-
vanyle
- Messages: 4
- Enregistré le: 10 Mar 2015, 20:07
-
 par vanyle » 19 Avr 2015, 13:24
par vanyle » 19 Avr 2015, 13:24
D'autres aides ?

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 19 Avr 2015, 13:37
par WillyCagnes » 19 Avr 2015, 13:37
tu poses u=x donc u'=1
v=Vx racine de x
donc v'=1/(2Vx)
2/3(uv)'=2/3(u'v +v'u)= 2/3[Vx +x/(2Vx)]
2/3[2Vx(Vx) +x)/2Vx
1/3[2x+x)/Vx]
1/3(3x)/(Vx)
x/Vx
=(Vx) donc tu avais bon

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 19 Avr 2015, 14:14
par zygomatique » 19 Avr 2015, 14:14
salut
sais-tu que tout nombre positif est le carré de sa racine carrée ??
et ton calcul est faux ....
 = \dfrac 2 3 \( \sqrt x + \dfrac x{2\sqrt x} \) = \dfrac 2 3 \( \sqrt x + \dfrac {\sqrt x}2 \) = \sqrt x)
ensuite comme on en comprend rien à ::
g(x) = (2/a)x avec a = e ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 175 invités