[TS] Nombres complexes - ensemble de points
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Whoever
- Messages: 9
- Enregistré le: 30 Aoû 2014, 14:57
-
 par Whoever » 12 Avr 2015, 14:51
par Whoever » 12 Avr 2015, 14:51
Bonjour,
Je bloque sur un énoncé que voici :
"Énoncé" a écrit:Dans un repère orthonormé direct
)
du plan complexe, on considère l'application

qui à tout point

d'affixe

où

associe le point
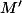
d'affixe
 L'ensemble des points
L'ensemble des points  tels que
tels que  est :
est :
- une droite privée d'un point
- un cercle privé d'un point
- une droite
- un cercle
C'est donc un QCM à une seule réponse possible. J'ai le corrigé non détaillé, il se trouve que la bonne réponse est la deuxième réponse :
un cercle privé d'un point.
Cependant, je n'arrive pas à trouver cette réponse ! Je trouve, pour ma part, que l'ensemble des points correspond à

.
Pouvez-vous m'aider en m'expliquant la démarche ?
Merci :lol3:
-
mathelot
 par mathelot » 12 Avr 2015, 17:08
par mathelot » 12 Avr 2015, 17:08
on note z* le conjugué de z.
)
( z' est imaginaire pur)

par produit en croix:
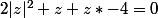
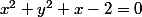
un cercle donc, privé de z=-2
l'homographie "mappe" un cercle sur une droite.
Plus généralement, l'ensemble des droites-cercles est conservé par les homographies..
-
Whoever
- Messages: 9
- Enregistré le: 30 Aoû 2014, 14:57
-
 par Whoever » 12 Avr 2015, 17:23
par Whoever » 12 Avr 2015, 17:23
Merci de ta réponse mathelot
Cependant, je n'ai pas compris tes calculs.
Que veux-tu représenter par ton astérisque ? Le conjugué ?
-
mathelot
 par mathelot » 12 Avr 2015, 17:24
par mathelot » 12 Avr 2015, 17:24
oui........................
On a écrit que z'=-z'*
la conjugaison est un morphisme de corps. on conjugue le quotient z'.
on obtient une expression quadratique (avec carrés)
qui se révèlent être une équation de cercle.
-
Whoever
- Messages: 9
- Enregistré le: 30 Aoû 2014, 14:57
-
 par Whoever » 12 Avr 2015, 17:30
par Whoever » 12 Avr 2015, 17:30
Sauf erreur de ma part :

Non ?
-
mathelot
 par mathelot » 12 Avr 2015, 17:36
par mathelot » 12 Avr 2015, 17:36
non
................. }=\dfrac{ \overline{z}-\bar{1}}{\overline{z}+\bar{2}})

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 12 Avr 2015, 17:57
par zygomatique » 12 Avr 2015, 17:57
salut
en notant z* le conjugué de z ....
on veut ::
(z* + 2) = -(z* - 1)(z + 2) 2zz* + z + z* - 4 = 0 4zz* + 2z + 2z* - 8 = 0 \\ (2z + 1)(2z* + 1) = 9 IM^2 = \(\dfrac 3 2\)^2)
où I est le point d'affixe

et on prend tous les points du cercle de centre I et de rayon 3/2 sauf celui d'affixe -2
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Whoever
- Messages: 9
- Enregistré le: 30 Aoû 2014, 14:57
-
 par Whoever » 13 Avr 2015, 11:35
par Whoever » 13 Avr 2015, 11:35
Bonjour zygomatique, merci pour ta réponse.
D'accord pour l'équation.
Cependant si
)
centre du cercle, et
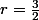
le rayon, alors il me semble que le point d'affixe -2 ne passe pas sur le cercle.
Pourquoi dit-on alors que le cercle est privé d'un point ?
-
mathelot
 par mathelot » 13 Avr 2015, 11:49
par mathelot » 13 Avr 2015, 11:49
Whoever a écrit:Bonjour zygomatique, merci pour ta réponse.
D'accord pour l'équation.
Cependant si
)
centre du cercle, et
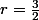
le rayon, alors il me semble que le point d'affixe -2 ne passe pas sur le cercle.
Pourquoi dit-on alors que le cercle est privé d'un point ?
excellente question qui doit te faire suspecter une erreur de calcul
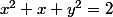
^2+y^2=\frac{9}{4})
le cercle est de centre
)
, de rayon 3/2, et il contient le point d'affixe -2

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 13 Avr 2015, 17:50
par zygomatique » 13 Avr 2015, 17:50
Whoever a écrit:Bonjour zygomatique, merci pour ta réponse.
D'accord pour l'équation.
Cependant si
)
centre du cercle, et
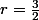
le rayon, alors il me semble que le point d'affixe -2 ne passe pas sur le cercle.
Pourquoi dit-on alors que le cercle est privé d'un point ?
oui l'affixe du point I est -1/2 ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
du plan complexe, on considère l'application
qui à tout point
d'affixe
où
associe le point
d'affixe
tels que
est :
