Bonjour à tous,
Nouvelle sur ce Forum, je viens chercher un peu d'aide sur un problème sur lequel je me casse les dents depuis plus de 2 semaines.
En voici l'énoncé.
Soit

un

-espace vectoriel de dimension finie

dont on note
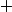
l'addition et soit
)
tel que
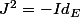
.
1) Montrer que

est un isomorphisme et

est un entier pair
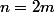
.
2) Soit

un élément non nul de

. Montrer que

et

sont linéairement indépendants.
3) Montrer qu'il existe une base de

de la forme
)
et donner l'expression de

dans cette base.
4) Déterminer les valeurs propres et les sous-espaces propres d'un tel endomorphisme

.
5) Mettre sur le groupe
)
une structure de

-espace vectoriel de dimension

Et voilà ce que j'ai bricolée!!!
1) Je n'ai pas réussi à prouver que

est un isomorphisme, mais puisque
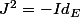
, on a
^2=(-1)^{dimE}=(-1)^n)
donc forcément

est pair donc
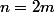
.
2) J'ai écrit pour
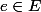
et pour tout
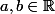
on a
e= ae+bJe)
3)???
4) Je pense que

annule le polynôme
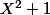
. Les valeurs propres de

sont donc à choisir parmi les racines de -1 dans

. Donc

et son opposé.
Merci d'avance pour votre aide
Bises Clara
