Aire et Intégrale

[Dwarfs43]

Bonjour, j'aurais besoin d'aide pour un exercice, le voici :

une demi parabole d’équation . Pour tout est une suite arithmétique dont on montre le premier terme et la raison .
Voici la figure :




Pour le moment j'aurais l'aire qui est égal à :



Mais je bloque déjà...

[Ncdk]

Pour le moment j'aurais l'aire qui est égal à :



Mais je bloque déjà...

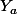
Je suppose que ton c'est le côté du quadrilatère, du moins ça hauteur ?
Sinon, dans ton intégrale quelque chose d'évident ce simplifie.

[Dwarfs43]

Hmm je ne vois pas se qui se simplifie, l'integral fait :


Mais je ne vois toujours pas se qu'il faut faire

[WillyCagnes]

bsr

entre les bornes n et n+1 on obtient:

[(n+1)^3 -n]/12 - n²/4

[(n+1)^3 -3n² -n]/12

[Dwarfs43]

c'est à dire entre les bornes, on est bien d'accord que l'air c'est :

[Ncdk]

Il y a pas de piège :zen:

Et je suis d'accord avec ton intégrale en effet.

[Dwarfs43]

Ah ok tout simplement
Donc on retombe sur

Soit

Donc l'aire est égale à


= ??

[Ncdk]

N'oublie pas que ta borne A c'est n et ta borne C c'est n+1, donc tu intègres entre n et n+1.

Donc ça revient à ce qu'a dis willy au final, grossièrement nous on a calculer l'aire totale - l'aire du quadrilatère mais tu pouvais carrément calculer l'aire totale sans passer par l'aire orange, mais tout dépend de ce que tu veux en faire après.

De plus ton calcul précédent est faux car c'est tes bornes que tu remplaces par x.

[Dwarfs43]

Ah oui, donc
= donc là c'est notre SA ?

[Ncdk]

Non tu dois plus avoir de x.

Tu dois faire : F(n+1)-F(n) où F(x) est ta primitive.

[Dwarfs43]

Hmm ok mais pourquoi on primitive ?

[Ncdk]

C'est le principe même du calcul d'intégrale ;)

[mathelot]

Hmm ok mais pourquoi on primitive ?

si f est continue,
est dérivable et sa dérivée est f

[Dwarfs43]

Non tu dois plus avoir de x.

Tu dois faire : F(n+1)-F(n) où F(x) est ta primitive.

= ? (j’avoue que je suis un peu perdu là)

[WillyCagnes]

relis donc ma réponse....