Angles de droites

[chan79]

si on a:
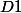
une droite , dirigée par un vecteur unitaire u1
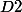
une droite , dirigée par un vecteur unitaire u2
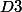
une droite , dirigée par un vecteur unitaire u3
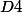
une droite , dirigée par un vecteur unitaire u4
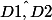
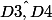
Pour savoir si et sont égaux,

il faut écrire la matrice M de la rotation qui transforme u1 en u2, et la matrice M' de la rotation qui transforme u3 en u4.

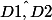
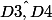
et sont égaux, si M=M' ou M+M'=matrice nulle (si les coefficients sont opposés, les angles diffèrent de )

[mathelot]

merci..........

[Robic]

Je me rends compte que je me suis laissé embrouiller tout seul hier en me basant sur a et Pi - a (qu'est-ce qui m'a pris ?). Mais non, les deux possibilités sont a et a - Pi, ce qui n'est pas du tout la même chose puisque a - Pi = a + Pi (modulo 2Pi), donc en effet on passe d'une rotation d'angle a à une rotation d'angle a + Pi en multipliant par -Id.

Et en plus tu l'avais bien expliqué :

Il est clair que pour aller de D1 à D2 de l'autre côté, on parcourt l'angle géométrique . Seulement, cet angle là est de sens opposé à . il vaut donc

[barbu23]

mathelot :

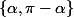
Si tu quotientes peut être par un sous groupes particulier : à trouver, tu auras peut être une correspondance bijective entre : et avec : la surjection canonique. Je t'ai expliqué ça plus haut. A toi de voir si ça peut marcher ou non. :happy3:

Cordialement. :happy3:

[barbu23]

mathelot :

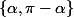
Si tu quotientes peut être par un sous groupes particulier : à trouver, tu auras peut être une correspondance bijective entre : et avec : la surjection canonique. Je t'ai expliqué ça plus haut. A toi de voir si ça peut marcher ou non. :happy3:

Cordialement. :happy3:

[mathelot]

oui, je pense que ça marche et les droites épointées sont des éléments de PSO(2,R) (cf. infra)

[zygomatique]

salut

de mémoire .... de plus en plus défaillante ...

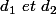
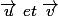
soit deux droites et un vecteur directeur respectif

alors il me semble

et plus précisément deux angles des droites d_1 et d_2 sont égaux ou supplémentaires ... (modulo pi)

[barbu23]

Bonjour, :happy3:

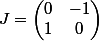
Si je peux me permettre, j'aimerais signaler à mathelot qu'on peut rendre la matrice plus simple qu'on peut le croire, en remarquant que : avec : ( cela sert à simplifier le maniement des formules par la suite, en calcul )

Cordialement. :happy3:

[paquito]

En remarquant que ; bien sûr! c'est un résultat qu'on utilise tous les jours!
, ça done ???

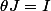
Faut pas dire n'importe quoi! prenons, d'oùet .

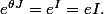
Revenons à des choses sérieuses, un angle de droite est la donnée d'un couple d'angles unitaire ; ce que l'on peut exprimer en termes d'angles de demi-droites, de matrices opposées ou encore en termes de complexes de modules 1.

Ce qui me semble important, c'est la somme d''angles de droites et on obtient tous les résultats utiles en montrant que l'ensemble des angles de droites est un groupe isomorphe au groupe des angles de demi-droites.