Proba
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
the_bongker
- Messages: 7
- Enregistré le: 04 Fév 2015, 02:19
-
 par the_bongker » 19 Fév 2015, 03:43
par the_bongker » 19 Fév 2015, 03:43
Je me demande quelle formule utiliser pour résoudre ce problème: On sait qu'en moyenne 6,7 voitures arrivent chaque heure à la fenêtre du guichet extérieur d'une banque.
Quelle est la probabilité qu'au plus 5 voitures arrive dans la prochaine heure?
Merci
-
mathelot
 par mathelot » 19 Fév 2015, 06:03
par mathelot » 19 Fév 2015, 06:03
il s'agit d'une loi de Poisson de paramètre

:
Soit

le nombre de véhicules arrivant dans l'heure
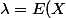)
Soit
= \sum_{k=0}^{5} \, \frac{ \lambda^k}{k!} e^{- \lambda})
avec

 \sim 0.340649)
-
the_bongker
- Messages: 7
- Enregistré le: 04 Fév 2015, 02:19
-
 par the_bongker » 19 Fév 2015, 06:08
par the_bongker » 19 Fév 2015, 06:08
mathelot a écrit:il s'agit d'une loi de Poisson de paramètre

:
Soit X le nombre de véhicules arrivant dans l'heure
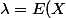)
Soit
= \sum_{k=0}^{5} \, \frac{ \lambda^k}{k!} e^{- \lambda})
avec

Si j'additionne les résultats de probas jusqu'à 5 à partir de la table de poisson, je devrait avoir le meme résultat que la formule?
-
mathelot
 par mathelot » 19 Fév 2015, 06:13
par mathelot » 19 Fév 2015, 06:13
the_bongker a écrit:Si j'additionne les résultats de probas jusqu'à 5 à partir de la table de poisson, je devrait avoir le meme résultat que la formule?
oui, regardons si ça donne le même résultat .
-
the_bongker
- Messages: 7
- Enregistré le: 04 Fév 2015, 02:19
-
 par the_bongker » 19 Fév 2015, 06:20
par the_bongker » 19 Fév 2015, 06:20
mathelot a écrit:oui, regardons si ça donne le même résultat .
0.3406 dans ma table. Donc loi de poisson c'est lorsque qu'il y a une intervalle de temps ou de longueur? Merci bcp
-
mathelot
 par mathelot » 19 Fév 2015, 07:29
par mathelot » 19 Fév 2015, 07:29
c'est la loi de proba des "évènements rares" (un client tous les dix minutes).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
