Probabilité DM

[laurent.2nd10]

Voici l'énoncé de mon problème.
Le duc de Toscane était un grand amateur de jeux de dés. A force de jouer, il lui semblait avoir remarqué qu'en lançant trois dés et en additionnant les points obtenus, il obtenait plus souvent 10 points que 9 points. Il n'arrivait pas à comprendre pourquoi parce que selon lui, il y avait autant de chances d'avoir l'un ou l'autre des deux résultats, chacun pouvant être obtenu de six façons différentes :
9 = 1+2+6 = 1+3+5 = 1+4+4 = 2+2+5 = 2+3+4 = 3+3+3
10 = 1+3+6= 1+4+45 = 2+2+6= 2+3+5 = 2+4+4= 3+3+4

L'objectif de l'exercice est de simuler un grand nombre de lancers de trois dés pour tester l'observation du Duc de Toscane.

1/a/ En complétant l'arbre ci-dessous, justifiez qu'il y a 36 issues possibles lorsque le 1 sort pour le dé 1.

b/ Déduisez-en le nombre d'issues possibles de l'expérience.

2/a/ En complétant l'arbre ci-dessous qui représente les différentes façons d'obtenir une somme égale à 9 avec les trois dés, dénombrez les issues favorables à l'évènement "obtenir 9".

b/ Dénombrez de la même façon les issues favorables à l'évènement "obtenir 10".

3/a/ Calculez les probabilités des deux évènements "obtenir 9" et "obtenir 10".
Sont-elles égales ?

b/ Expliquez l'erreur de raisonnement qu'a commise le Duc de Toscane.

[mathelot]

bonour,

effetivement , "la somme des points égale 9" ou "la somme des points égale 10"
comporte le même nombre d'éléments, en fait de classes de la partition.


En tout, il y a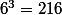 possibilités.

je liste la partition associée à "somme des points égale 10"

"1+3+6" comporte 3!=6 éléments
"1+4+5" comporte 3!=6 éléments
"2+2+6" comporte 3 éléments

etc.

pour ne pas avoir de doublons dans les classes, il faut choisir les termes de la
somme croissant au sens large, comme si c'était des arrangements.

je trouve 33 triplets pour le 10 , 25 triplets pour le 9, et le paradoxe
fait que les deux partitions ont même nombre de classes:6

Bonne journée.

[mathelot]

l'écriture formelle "1+3+6"
indique 3!=6 façons de les placer

"2+2+6" indique 3 façons de les placer

"3+3+3" indique une seule façon de les placer

[mathelot]

apparemment, 27 triplets pour la classe "somme des points =10"

[laurent.2nd10]

Ha ok. Merci' ;);)