Exercice relation d'ordre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 22 Jan 2015, 20:38
par Rik95 » 22 Jan 2015, 20:38
Bonsoir,
Quelqu'un pourrai m'expliquer comment résoudre la 2eme et 3eme question de cette exercice svp, je suis complètement perdu

Merci
-
Wataru
- Membre Naturel
- Messages: 24
- Enregistré le: 29 Aoû 2014, 16:11
-
 par Wataru » 22 Jan 2015, 20:48
par Wataru » 22 Jan 2015, 20:48
Salut,
R est une relation d'ordre.
Comment peut-on traduire "n est un élément minimal pour R" avec des assertions ?
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 22 Jan 2015, 21:50
par Rik95 » 22 Jan 2015, 21:50
je dirai que m est un élément minimal si m<=n
-
Wataru
- Membre Naturel
- Messages: 24
- Enregistré le: 29 Aoû 2014, 16:11
-
 par Wataru » 22 Jan 2015, 23:56
par Wataru » 22 Jan 2015, 23:56
Qui est n ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 23 Jan 2015, 00:20
par zygomatique » 23 Jan 2015, 00:20
salut
que penser de 1 ? d'un nombre premier ?
peux-tu comparer 3 et 6 ? 3 et 9 ? et plus généralement
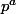
et
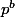
?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 23 Jan 2015, 12:33
par Rik95 » 23 Jan 2015, 12:33
Bah n représente tout les nombre appartenant a N*.
1 est un élement minimal car il n'y a pas plus petit que lui dans N*, pour l'élement maximal je pense qu'il n'existe pas car N* car aucun nombre de N* est plus grand que tout les autres ...
pour 3 et 6 , on ne peu pas les comprer car 6 ne peu pas s'ecrire sous la forme de 3^k, pour 3 et 9 on peut.
Parcontre je ne vois pas le rapport avec les nombres premiers ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 23 Jan 2015, 21:08
par zygomatique » 23 Jan 2015, 21:08
1 est un élement minimal car il n'y a pas plus petit que lui dans N*,
comment sais-tu qu'il n'y a pas plus petit ? plus grand ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 23 Jan 2015, 23:40
par Rik95 » 23 Jan 2015, 23:40
car dans l'ensemble N* commence a partir de 1, tout les autres éléments de cet ensemble sont plus grand que lui
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 24 Jan 2015, 08:25
par BiancoAngelo » 24 Jan 2015, 08:25
Rik95 a écrit:car dans l'ensemble N* commence a partir de 1, tout les autres éléments de cet ensemble sont plus grand que lui
Bonjour,
Il semblerait que tu ne saisisses pas la subtilité. Il faut que tu le démontres. Avec cette relation d'ordre.
Montre que 1 est plus petit que tous les autres
avec cette relation d'ordre (si du moins c'est le cas).
Sinon, quel est l'intérêt de l'exercice ?
Sais-tu la définition d'élément minimal ? D'élément maximal ?
Si oui, démontre les choses correctement avec celles-ci.
As-tu saisi comment fonctionne ta relation d'ordre ? Ce que ça signifie qu'elle soit partielle ?
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 24 Jan 2015, 10:37
par Rik95 » 24 Jan 2015, 10:37
Ok je vois :S, oui je pense avoir saisi pourquoi la relation est partielle, c'est parce que on ne peu pas l'appliquer a tous les nombres, parcontre la relation est une égalité ... n = m^k , je ne vois pas trop comment je peu le montrer du coup ...
Si je prend le cas ou n = 1, on a également m = 1 car 1^k est toujours egal a 1, dans ce cas on peut dire que 1 est un élement minimal car il n'y a pas plus petit que lui.
Dans les autres cas, si on prend tout les autres nombres supérieur a 1, on a n = m^k qui ne s'applique pas a tout les nombres ... si je prend par exemple n = 2 alors m = 2, si je prend n= 3 je peu pas appliquer la relation ...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 10:50
par zygomatique » 24 Jan 2015, 10:50
Rik95 a écrit:car dans l'ensemble N* commence a partir de 1, tout les autres éléments de cet ensemble sont plus grand que lui
1 "est plus petit que" 2 pour la relation < (ou =<)
mais ce n'est pas cette relation que tu utilises !!!!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 24 Jan 2015, 12:49
par Rik95 » 24 Jan 2015, 12:49
Je définie le plus petit élément en fonction de quoi alors ? pourrai tu me donner un exemple avec cette relation stp ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 13:27
par zygomatique » 24 Jan 2015, 13:27
ben en fonction de ta relation d'ordre !!!
en notant T cette relation
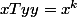
pour un certain k
je t'ai donné des exemples !!!
quand a-t-on

?

?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 24 Jan 2015, 14:28
par Rik95 » 24 Jan 2015, 14:28
pour x = 1, mais comment je démontre qu'il n'y a pas plus petit que lui ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 15:02
par zygomatique » 24 Jan 2015, 15:02
Rik95 a écrit:pour x = 1, mais comment je démontre qu'il n'y a pas plus petit que lui ?
mais un peu de sérieux !!!
quelle est la différence entre un pigeon ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 24 Jan 2015, 15:21
par Rik95 » 24 Jan 2015, 15:21
Comment ça ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 15:49
par zygomatique » 24 Jan 2015, 15:49
Rik95 a écrit:Comment ça ?
quelle est la différence entre un pigeon ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
dlzlogic2
- Membre Naturel
- Messages: 38
- Enregistré le: 06 Oct 2014, 12:40
-
 par dlzlogic2 » 24 Jan 2015, 15:58
par dlzlogic2 » 24 Jan 2015, 15:58
zygomatique a écrit:quelle est la différence entre un pigeon ?
Y'en a pas, les deux ailes c'est pareil, surtout la gauche. :dodo:
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 24 Jan 2015, 16:18
par Rik95 » 24 Jan 2015, 16:18
quel est le rapport ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 17:26
par zygomatique » 24 Jan 2015, 17:26
Rik95 a écrit:quel est le rapport ?
quelle est la différence entre un pigeon ?
1 est-il plus grand qu'une pomme ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités

