Bonjour à tous.
Je vous fais part d'un problème de probabilités qui me donne du fil à retordre. Mais je ne maîtrise pas bien les probabilités. Ou du moins, ça fait trop longtemps que j'ai quitté les bancs de l'école !
Soit une suite de variables aléatoires de Bernouilli indépendantes X0.... Xn... qui valent toutes 1 avec la probabilité p et 0 avec la probabilité 1-p.
Soit Sn la variable aléatoire égale à la somme des variables X0 à Xn.
Quelle est l'espérance du produit 3^Sn . Xn ?
Je vous remercie d'avance pour vos lumières.
Espérance et variables de bernouilli
12 messages
- Page 1 sur 1
Terras a écrit:Bonjour à tous.
Je vous fais part d'un problème de probabilités qui me donne du fil à retordre. Mais je ne maîtrise pas bien les probabilités. Ou du moins, ça fait trop longtemps que j'ai quitté les bancs de l'école !
Soit une suite de variables aléatoires de Bernouilli indépendantes X0.... Xn... qui valent toutes 1 avec la probabilité p et 0 avec la probabilité 1-p.
Soit Sn la variable aléatoire égale à la somme des variables X0 à Xn.
Quelle est l'espérance du produit 3^Sn . Xn ?
Je vous remercie d'avance pour vos lumières.
Bonsoir,
Je pense que d'abord, il faut établir la loi de probabilité de la somme
Vu qu'on a une suite de variables aléatoires de Bernouilli indépendantes qui prennent 0 ou 1 comme valeurs et qu'en plus les paramètres sont identiques, ça revient à regarder une seule de ces variables et compter le nombre de fois où elle vaut 1 pour savoir quand est-ce que que
Tout ça pour dire que je pense que ta somme
Pour être plus clair,
Maintenant, il faut bien voir que
Donc
Or,
Maintenant on a
D'où
D'où :
D'où :
Donc on a :
Et finalement :
Voilà, j'espère ne pas avoir fait d'erreurs...
BiancoAngelo a écrit:Bonsoir,
Je pense que d'abord, il faut établir la loi de probabilité de la somme.
Vu qu'on a une suite de variables aléatoires de Bernouilli indépendantes qui prennent 0 ou 1 comme valeurs et qu'en plus les paramètres sont identiques, ça revient à regarder une seule de ces variables et compter le nombre de fois où elle vaut 1 pour savoir quand est-ce que quevaut un certain
.
Tout ça pour dire que je pense que ta sommesuit une loi binomiale de paramètre n et p.
Pour être plus clair,
Maintenant, il faut bien voir quetransforme
"sympathiquement", puisque à une unique valeur
est associée une valeur
et vice versa.
Donc
Or,car les deux variables
et
sont indépendantes.
Maintenant on a
D'où
D'où :
D'où :
Donc on a :
Et finalement :
Voilà, j'espère ne pas avoir fait d'erreurs...
Bonsoir, et merci beaucoup pour votre réponse, très précise. J'aurais quelques commentaires. Je pense effectivement que la loi de la somme est binomiale. Cependant la somme comporte non pas n, mais n+1 termes. Donc il me semble que
D'où :
Or,
Je suis d'accord sur l'indépendance de
La quantité
* car
Mais bien évidement, cette probabilité n'a pas d'influence sur le calcul de l'espérance, puisqu'elle est multipliée par la valeur 0.
En tout cas, merci beaucoup pour vos éclaircissements.
Bonjour ! Bien vu... Pfff, commencer par un erreur :ptdr: enfin, au moins ça montrait bien le chemin !
Je note tout, comme ça, je vérifie en relisant ce que je corrige.
 = \binom{n+1}{k} p^k(1-p)^{n+1-k})
Donc = \binom{n+1}{k} p^k(1-p)^{n+1-k})
Or, = P(S_n = k \cap X_n = 1) = P(S_{n-1} = k-1 \cap X_n =1) = p \binom{n}{k-1} p^{k-1}(1-p)^{n-(k-1)}) car les deux variables
car les deux variables 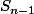 et
et  sont indépendantes.
sont indépendantes.
Maintenant on a = \sum 3^k P(3^{S_n} X_n = 3^k) = \sum\limits_{k=1}^{n+1} 3^k \times p \binom{n}{k-1} p^{k-1}(1-p)^{n-(k-1)})
D'où^{n-(k-1)})
D'où^{n-k})
D'où^{k}(1-p)^{n-k})
D'où^n }) .
.
Donc je suis d'accord avec toi (tu tombes sur les bons résultats, mais tu as fait des oublis quand même dans l'écriture des calculs, notamment le fait que k aille justement jusque n+1, et une faute sur la dernière ligne avec la puissance)!
Sinon, oui, je n'ai pas calculé la probabilité de faire 0, vu qu'elle n'intervient pas dans l'espérance.
Et pareil, dans le calcul avec l'intersection, k= 0 n'est pas possible car il faut au moins que X_n vaille 1 !
Je note tout, comme ça, je vérifie en relisant ce que je corrige.
Donc
Or,
Maintenant on a
D'où
D'où
D'où
D'où
Donc je suis d'accord avec toi (tu tombes sur les bons résultats, mais tu as fait des oublis quand même dans l'écriture des calculs, notamment le fait que k aille justement jusque n+1, et une faute sur la dernière ligne avec la puissance)!
Sinon, oui, je n'ai pas calculé la probabilité de faire 0, vu qu'elle n'intervient pas dans l'espérance.
Et pareil, dans le calcul avec l'intersection, k= 0 n'est pas possible car il faut au moins que X_n vaille 1 !
Terras a écrit:J'en aurais un autre du même genre. Quelle est l'espérance de la quantité 3^(2Sn-Sq) . Xn, où q<=n.
Si n=q on se ramène au cas précédent.
Si q < n alors S_n et S_q sont indépendantes et on a:
On calcule l'espérance de
mrif a écrit:Si n=q on se ramène au cas précédent.
Si q < n alors S_n et S_q sont indépendantes et on a:
On calcule l'espérance deen utilisant la méthode proposée par BiancoAngelo, et comme le numérateur et le dénominateur sont 2 variables indépendantes et que le dénominateur est non nul, l'espérance du quotient est égale au quotient des espérances.
Bonsoir, ça ferait :
Et pourquoi sont-elles indépendantes ? Il y a le "début" de la somme dans chacune, non ?
Terras a écrit:J'en aurais un autre du même genre. Quelle est l'espérance de la quantité 3^(2Sn-Sq) . Xn, où q<=n.
Je pense qu'on doit écrire (dans le cas q <n) :
Soit
avec
D'où
D'où
On a donc
Et il y a des chances qu'on trouve
Car si q = n-1, on
Et alors,
Voilà, en espérant, encore une fois, ne pas avoir fait d'erreur et une conjecture correcte (vus tous les calculs réalisés en première partie).
PS : mrif, même choix pour S' :zen:
Bonsoir, je vois que mon petit problème a fait phosphorer les esprits brillants. En effet, le découpage en deux sommes disjointes me semble être la bonne méthode. Les deux sommes sont de fait indépendantes entre elles, bien que l'une d'elle (et l'une d'elle seulement) soit dépendante de la variable Xn. Mais le premier exercice permet de résoudre ce cas. Merci à l'ange blanc pour son aide précieuse.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 110 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
