Logarithmes

[chamarie]

Bonsoir !

J'ai plusieurs exercices sur les logarithmes, je n'en avais jamais fais auparavant, ayant fais un bac st2s, et j'aurais voulu savoir si mes réponses sont exact, Merci

Le premier exercices: résoudre les équations ou inéquations,

1. e^4x-2e^3x=0
2. e^2x-4e^x<0

1. e^4x-2e^3=0
e4x=2e^3x
ln(e^4x)=2 ln(e^3x)
4x= 2*3x
4x=6x
x^2=6-4
x^2=2
x(racine)2
S= ( x(racine)2 )

2.e^2x-4e^x<0
ln(e^2x)-4ln(e^x)
2x-4x<0
2x<0


exercice 6

simplification

1. ln2x+ln3
2. ln(2x+2)-ln(x+1)
3.(ln(2x+1)+ln2)^2

1. ln2x+ln3 = ln(2x*3)= ln6x= 6x
2. ln(2x+2)-ln(x+1)= ln (2x+2/x+1) = ln (4x/2x)= 2
3. (ln(2x+1)+ln2)^2 = (ln(2x+1)+ln2)+(ln(2x+1)+ln2)=
ln(6x)+ln(6x)
ln(6x*6x)
ln(36x)= 36x

[BiancoAngelo]

Bonsoir !





Après je ne sais pas non plus d'où sort ton x².

Bref, utilise pour le côté droit de l'équation.

Et après c'est du premier degré (je ne sais vraiment pas pourquoi tu avais mis du x²).

[annick]

Bonjour,

il y a une façon rapide de faire :

e^4x-2e^3x=0

On met en facteur e^3x, soit :

e^3x(e^x-2)=0

e^3x jamais nul, donc une seule solution e^x-2=0 d'où e^x=2, x=ln 2

[chamarie]

Merci, pour votre aide :we: , pour mes autres éuations, est ce que cela est juste ?

[Carpate]

Merci, pour votre aide :we: , pour mes autres équations, est ce que cela est juste ?

Pour le 2) : lincorrect dès la deuxième ligne
Procède comme pour le 1) :


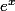
Sachant que est positif sur R :


Pour la suite utilise :
ln(ab) = lna + lnb
ln(a/b) = lna -lnb

[chamarie]

Pour le 2) : lincorrect dès la deuxième ligne
Procède comme pour le 1) :


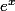
Sachant que est positif sur R :


Pour la suite utilise :
ln(ab) = lna + lnb
ln(a/b) = lna -lnb

Dac c'est Ok merci !

Pour mes simplification ln(6x) c'est bien égale à 6 ?