Quadriques

par **MacManus** » 30 Avr 2008, 18:56

Bonsoir,

Déterminer la nature des quadriques déquations cartésiennes :

Ces quadriques contiennent-elles des droites?

Est-ce que je dois développer et simplifier ces 2 expressions pour reconnaître ces quadriques, ou est-ce qu'il existe une méthode plus simple ??

la 1ère expression ressemble à une forme quadratique (carrés de Gauss?)
Merci de bien vouloir me guider!

par **XENSECP** » 01 Mai 2008, 09:43

Je crains qu'il ne faille développer ^^

par **alavacommejetepousse** » 01 Mai 2008, 09:55

bonjour

il suffit de faire un changement de repère
le genre de la quatrique ne change pas

par **XENSECP** » 01 Mai 2008, 10:00

AH c'est pas faux ^^ En plus ça se voit effectivement ^^

Hyperboloide 1 nappe le premier

par **MacManus** » 01 Mai 2008, 10:36

Bonjour bonjour,

Bon effectivement je peux toujours développer j'ai essayé ms ca ne me parle pas trop. Pour être franc je n'ai pas vraiment étudier les quadriques en cours par contre je crois me souvenir que l'hyperboloïde à 1 nappe qui a pour équation, je pense :

..?
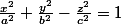
(en particulier avec a = b = c =1)....

changer de repère : cela signifie-t-il qu'il faut que je passe en cylindrique...?

merci beaucoup!!

par **XENSECP** » 01 Mai 2008, 10:38

mais non tu pose X = x+y+2z, Y=x-y+z et Z=x+y ;)

par **MacManus** » 01 Mai 2008, 10:41

Ah oui d'accord je comprend l'idée du changement de repère (pas de coordonées)
MERCI

par **hgilles06** » 24 Nov 2014, 21:04

Bonsoir chers amis. pouvez vous m'aider ? on me demande la nature de cette forme quadratique selon les valeurs de a :
q(xyz)= (a^2)x^2 + (1-a)y^2 + (2-a)z^2-2axy +2axz + 2(a-1)yz

Quadriques

Quadriques

Qui est en ligne