Problème exercice de Divisibilité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
spit
- Membre Naturel
- Messages: 35
- Enregistré le: 26 Sep 2010, 14:06
-
 par spit » 02 Nov 2014, 18:56
par spit » 02 Nov 2014, 18:56
Bonjour,
Dans un exercice de divisibilité je dois compléter un algorithme mais je suis complètement bloqué.
Voici l'énoncé:
A(n)=5^n-1
L'Algorithme:
Entrée: Saisir N
Traitement: A prend la valeur 5^n-1
Q prend la valeur de la partie entière de A/...
R prend la valeur A-...
Sortie: R
On me demande de compléter cet algorithme pour qu'il affiche les deux derniers chiffres de l'entier A(n)
J'ai essayer avec n=5, ce qui me fait A=3124, donc l'algorithme devrait m'afficher 24
J'ai fait:
-Q prend le valeur de la partie entière de A/N
-R prend la valeur A-(QxN)
Ce qui me donne 4.
Donc ce n'est pas encore ça.
Merci d'avance.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 02 Nov 2014, 20:21
par zygomatique » 02 Nov 2014, 20:21
salut
Q prend la .... de A/100
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
spit
- Membre Naturel
- Messages: 35
- Enregistré le: 26 Sep 2010, 14:06
-
 par spit » 03 Nov 2014, 18:25
par spit » 03 Nov 2014, 18:25
zygomatique a écrit:salut
Q prend la .... de A/100
Salut,
En faisant ceci Q serait égal a 31. et ce n'est pas 24 que je veux ?
Que faudrait-il faire à la ligne suivante pour R ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 03 Nov 2014, 18:51
par chan79 » 03 Nov 2014, 18:51
spit a écrit:Salut,
En faisant ceci Q serait égal a 31. et ce n'est pas 24 que je veux ?
Que faudrait-il faire à la ligne suivante pour R ?
Pour obtenir 24 il faut retrancher à 3124 le nombre 100*Q
-
spit
- Membre Naturel
- Messages: 35
- Enregistré le: 26 Sep 2010, 14:06
-
 par spit » 06 Nov 2014, 21:16
par spit » 06 Nov 2014, 21:16
Merci ca marche.
Je bloque encore pour deux questions faisant partie du même exercice:
1) Démontrer que pour tout entier n, A(n) est divisible par 4
2) Vérifier que pour tout entier n>2,5^n-25 = 25xA(n-2)
Merci d'avance.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Nov 2014, 21:31
par chan79 » 06 Nov 2014, 21:31
spit a écrit:Merci ca marche.
Je bloque encore pour deux questions faisant partie du même exercice:
1) Démontrer que pour tout entier n, A(n) est divisible par 4
Merci d'avance.
tu as une formule;
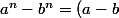(\...\ ))
ou alors récurrence
si
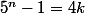
-1)
qui est multiple de

l'initialisation ne pose pas de difficulté
-
spit
- Membre Naturel
- Messages: 35
- Enregistré le: 26 Sep 2010, 14:06
-
 par spit » 06 Nov 2014, 21:50
par spit » 06 Nov 2014, 21:50
Bonjour,
Merci c'est deja un peu plus simple avec la récurrence, je pensais partir sur des congruences mais ce n'est pas utile.
Par contre pour ce qui est de la question 2, je cale complétement.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Nov 2014, 00:15
par fatal_error » 07 Nov 2014, 00:15
pour la 2
2) Vérifier que pour tout entier n>2,5^n-25 = 25xA(n-2)
5^n = 25*5^(n-2)
donc
5^n-25 = 25*5^(n-2) - 25 = 25*(5^(n-2) - 1)
la vie est une fête

-
spit
- Membre Naturel
- Messages: 35
- Enregistré le: 26 Sep 2010, 14:06
-
 par spit » 07 Nov 2014, 10:27
par spit » 07 Nov 2014, 10:27
fatal_error a écrit:pour la 2
5^n = 25*5^(n-2)
donc
5^n-25 = 25*5^(n-2) - 25 = 25*(5^(n-2) - 1)
Bonjour,
J'ai du mal a comprendre des la premiere ligne pourquoi 5^n=25*5^(n-2)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Nov 2014, 10:48
par fatal_error » 07 Nov 2014, 10:48
car 25=5^2 :/
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
