Exercice de révision (divisibilité)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 12 Aoû 2010, 00:21
par Dinozzo13 » 12 Aoû 2010, 00:21
Bonjour, je glisse ici un petit exercice d'arithmétique simple pour moi réviser ^^, merci de m'indiquer mes erreurs au cas où, merci.
Déterminer l'ensemble des entiers

tels que

.

est de degré 3 et

de degré 1, donc il existe un trinôme

tel que, pour tout

:
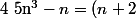f(n)+r)
où
=an^2+bn+c)
Pour tout

:
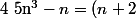f(n)+r)
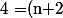(an^2+bn+c)+r)
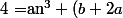n^2+(c+2b)n+2c+r)
Par identification, cela équivaut à :
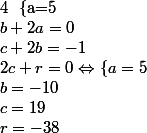
.
Donc pour tout

:
=5n^2-10n+19)
Et par conséquent,
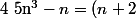(5n^2-10n+19)-38)
Or si

alors

.
Par conséquent,

si et seulement si

.
Etablissons l'ensemble des diviseurs de 38 :
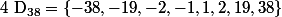
.
Par suite, pour tout

:

si et seulement si :
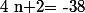
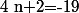
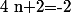
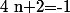
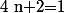
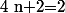
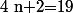
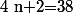
Donc par conséquent,

si et seulement si

Voilà, en espérant avoir été assez rigoureux ^^
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Aoû 2010, 11:21
par Nightmare » 12 Aoû 2010, 11:21
Salut !
La méthode est bonne. Petite erreur de vocabulaire : "donc il existe un trinôme tel que" , rien ne dit que c'est un trinôme, un polynôme du second degré par contre, c'est sûr :lol3:
Sinon, la méthode de division polynômiale est à retenir car très pratique :
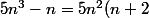-10n^2-n=5n^{2}(n+2)-10n(n+2)+19n=5n^{2}(n+2)+10n(n+2)+19(n+2)-38=(n+2)(5n^2+10n+19)-38)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 12 Aoû 2010, 14:51
par Dinozzo13 » 12 Aoû 2010, 14:51
Salut, oui, il était sous entendu qu le polynôme était de degré 3-1 donc 2, d'où le fait que je me suis contenté de dire trinôme.
En effet oui, pratique ta méthode aussi :++:
Merci
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Aoû 2010, 22:36
par Nightmare » 12 Aoû 2010, 22:36
Dinozzo13 a écrit:Salut, oui, il était sous entendu qu le polynôme était de degré 3-1 donc 2, d'où le fait que je me suis contenté de dire trinôme.
C'est bien ce qui me semblait, ma remarque était plus pour te dire qu'un trinôme n'est pas un polynôme du second degré, juste un polynôme ayant 3 monômes (donc peut être de degré 15 000 si on veut)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 13 Aoû 2010, 00:31
par Dinozzo13 » 13 Aoû 2010, 00:31
Ah bon, moi on m'a toujours dit qu'un polynôme de degré 2 était un trinôme :hum:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2010, 10:37
par Nightmare » 13 Aoû 2010, 10:37
Dinozzo13 a écrit:Ah bon, moi on m'a toujours dit qu'un polynôme de degré 2 était un trinôme :hum:
Ah ? Pas ton prof j'espère :lol3:
Surement as-tu entendu "trinôme du second degré", comme on le voit dans beaucoup de cours de première.
-
Anonyme
 par Anonyme » 13 Aoû 2010, 13:58
par Anonyme » 13 Aoû 2010, 13:58
Dinozzo, un exemple.
Considérons la fonction f définie sur R par :
f(x)=x²+1.
f est un polynôme du second degré, mais c'est un binôme.
Ce contre exemple te montre qu'il existe des polynômes du second degré qui ne soient pas des trinômes.
On appelle trinôme du second degré toute fonction de la forme f(x)= ax²+bx+c où (a,b,c) appartient à R*x R².
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2010, 14:02
par Nightmare » 13 Aoû 2010, 14:02
Titux a écrit:On appelle trinôme du second degré toute fonction de la forme f(x)= ax²+bx+c où (a,b,c) appartient à R*x R².
appartient à (R*)^3 plutôt, b et c ne peuvent pas être nuls, sinon, c'est plus un trinôme.
-
Anonyme
 par Anonyme » 13 Aoû 2010, 14:04
par Anonyme » 13 Aoû 2010, 14:04
Oui effectivement. Au fait une question Nightmare, quand tu écris (R*)^3 tu peux mettre le 3 en exposant et l'étoile en indice ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 13 Aoû 2010, 14:23
par Nightmare » 13 Aoû 2010, 14:23
Non, ce n'est pas conventionnel.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 13 Aoû 2010, 14:43
par Dinozzo13 » 13 Aoû 2010, 14:43
Nightmare a écrit:Ah ? Pas ton prof j'espère :lol3:
Surement as-tu entendu "trinôme du second degré", comme on le voit dans beaucoup de cours de première.
Ben il me semble que si.
En plus, je viens de vérifier dans mon ancien manuel de 1re S et il est clairement dit qu'un trinôme est un polynôme de degré 2.
C'est pas malin de leur part :hum:
Donc par exemple :

est aussi un trinôme.
Toutefois merci de cette précision :++:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 15 Aoû 2010, 01:32
par Dinozzo13 » 15 Aoû 2010, 01:32
Me revoilà pour une question :
Est-il vrai que si n est un entier alors quel que soit les entiers a,b,c et d, le quotient

n'admet que deux valeurs de n telles que

.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 15 Aoû 2010, 01:34
par Dinozzo13 » 15 Aoû 2010, 01:34
Me revoilà pour une question :
Est-il vrai que si n est un entier alors quel que soit les entiers a,b,c et d, le quotient

n'admet que deux valeurs de n telles que

?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 15 Aoû 2010, 01:48
par Dinozzo13 » 15 Aoû 2010, 01:48
Et de même si l'on considère 6 entiers a,b,c,d,e,f tels que :

Est-il vrai qu'il n'existe que 4 valeurs de n entières pour lesquelles ce quotient est entier ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 15 Aoû 2010, 09:36
par Finrod » 15 Aoû 2010, 09:36
Dinozzo13 a écrit:Me revoilà pour une question :
Est-il vrai que si n est un entier alors quel que soit les entiers a,b,c et d, le quotient

n'admet que deux valeurs de n telles que

?
A priori non. Par ex
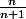
n'est jamais entier, sauf en 0.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 15 Aoû 2010, 14:26
par Dinozzo13 » 15 Aoû 2010, 14:26
Ben si pourtant, si n=0 ou si n=-2 alors le quotient est bien entier :hum:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 15 Aoû 2010, 16:07
par Finrod » 15 Aoû 2010, 16:07
EN effet, je pensais dans

.
Je pense que déjà il faut éliminer les cas ou ad-bc=0, car la fonction est alors constante.
Mais après ça demande un calcul.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 15 Aoû 2010, 16:25
par Dinozzo13 » 15 Aoû 2010, 16:25
Ah, oui. Je sous-entendais qu'on se trouvait dans l'ensemble des entiers (

).
Autre petite question :
Pourrais-t-on m'expliquer ce qu'est cela :

.
Car je ne comprends pas du tout cette signification.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 15 Aoû 2010, 18:56
par Finrod » 15 Aoû 2010, 18:56
En tant qu'ensemble , c'est les reste possible dans la division par n, donc 0...n-1.
Il y a ensuite une structure d'anneau induite par Z.
Car si deux nombre sot congrus à k et k' modulo n, leur somme sera congru à k+k' donc l'addition passe aux restes, i.e. à Z/nZ.
Idem pour la multiplication.
-
Benjamin
- Membre Complexe
- Messages: 2337
- Enregistré le: 14 Avr 2008, 10:00
-
 par Benjamin » 15 Aoû 2010, 19:28
par Benjamin » 15 Aoû 2010, 19:28
Ben314 avait fait un post assez complet à ce sujet.
Voir le #83 et la suite
ici.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
