DM Géomètrie dans l'espace

[drumsgirl]

bonjour,
j'ai ce DM à faire mais je bloque sur les questions.... :triste:
Pouvez vous m'aider svp ?
Merci
Emma :we:

Enoncé :
On considère un cube ABCDEFGH de côté a. On nomme I, J, K, L, M et N les centres respectifs des faces ABCD, BCGF, DCGH, ADHE, ABFE et EFGH.
1) Démontrer que LN= a racine de 2 divisé par 2

2) En déduire la nature des triangles coposant les huit faces du solide IJKLMN.

[Peacekeeper]

Bonsoir Emma,

Que pouvez-vous dire des droites (LN) et (DG)?

[drumsgirl]

Bonsoir Emma,

Que pouvez-vous dire des droites (LN) et (DG)?

Bonjour Peacekeeper et merci de votre réponse.
Les droites (LN) et (DG) sont parallèles (visuellement), mis comment le prouve t-on ? :/
et puis cela nous servira à quelque chose ?
merci
Emma

[Peacekeeper]

Je vous en prie.

Cela nous servira à appliquer le théorème de Thalès afin d'obtenir des informations sur LN. Et vous avez parfaitement raison il nous faut prouver qu'elles sont parallèles. Pour cela je vous suggère de regarder de près les triangles LNE et DGE ^^

[paquito]

Si l'on construit le triangle AFH, N est le milieu de [HF] et L celui de [HA], donc le théorème des milieux permet de conclure que
Ensuite il suffit de faire des rotations de 90° pour se rendre compte que NK, NJ et NM jouaient le même rôle que NL, puis que IJ,IL,IK et IM faisaient de même, enfin une autre rotation permet de voir que JK, KL, LM et MJ aussi.

Donc on fait un seul calcul, puis ensuite en manipulant le cube, on trouve que ,

donc IJKLMN est la réunion de 2 pyramides de base carrée et ses 8 faces sont des triangles équilatéraux (une sorte de "berlingot").

Il est clair que cet exercice doit être accompagnée d'une figure réalisé sur Géospace ou sur la dernière version de Géogébra que l'on peut télécharger sans problème.

[Peacekeeper]

Bravo paquito, bien joué. Je vous renvoie à la charte de Maths Forum:
http://www.maths-forum.com/announcement.php?f=14

"Note aux correcteurs :
Au cas par cas, lorsqu'il est avéré que l'élève est vraiment perdu dans la résolution d'un problème, qu'il respecte tous les points de la charte (politesse, etc.) et qu'il est de bonne foi (effort de recherche, volonté d'essayer, etc.), il est possible que le correcteur donne une réponse complète. Il est toutefois interdit de le faire si un autre intervenant est en cours d'échange avec l'élève. Dans tous les autres cas, il est demandé au correcteur de guider progressivement l'élève vers la résolution complète de son énoncé.

Lorsqu'un correcteur donne ipso facto la réponse complète à un élève sans que celui-ci n'ait fourni un effort de recherche ou ne paraisse complètement perdu, il est convenu que le modérateur le prévienne par message privé de son comportement contraire à la charte. Au delà de 3 manquements à la charte, le correcteur peut alors se voir sanctionner sous la forme d'une exclusion temporaire de 15 jours ou définitive si le correcteur ne modifie toujours pas son comportement."

[paquito]

Bravo paquito, bien joué. Je vous renvoie à la charte de Maths Forum:
http://www.maths-forum.com/announcement.php?f=14

"Note aux correcteurs :
Au cas par cas, lorsqu'il est avéré que l'élève est vraiment perdu dans la résolution d'un problème, qu'il respecte tous les points de la charte (politesse, etc.) et qu'il est de bonne foi (effort de recherche, volonté d'essayer, etc.), il est possible que le correcteur donne une réponse complète. Il est toutefois interdit de le faire si un autre intervenant est en cours d'échange avec l'élève. Dans tous les autres cas, il est demandé au correcteur de guider progressivement l'élève vers la résolution complète de son énoncé.

Lorsqu'un correcteur donne ipso facto la réponse complète à un élève sans que celui-ci n'ait fourni un effort de recherche ou ne paraisse complètement perdu, il est convenu que le modérateur le prévienne par message privé de son comportement contraire à la charte. Au delà de 3 manquements à la charte, le correcteur peut alors se voir sanctionner sous la forme d'une exclusion temporaire de 15 jours ou définitive si le correcteur ne modifie toujours pas son comportement."

Je n'ai en aucun cas fourni une réponse complète! L'élève doit déjà comprendre mes "rotations" ce qui est en fait "hors programme". quand à la solution finale, qui n'est pas du tout évidente, l'élève devra la justifier, ce qui n'est pas évident. Je préconise une figure Géoplan ou Géogébra mais la figure est difficile à faire. J'ai donc donné des indications proportionnelles à la difficulté de l'exercice. Si on comprend ce que j'appelle manipuler le cube, je crois que j'aurais fait travailler sérieusement l'élève (il n'y a rien d'évident).
Quant aux collègues qui répondent:"qu'à tu fait? ou "pense à thalès;( ici c'est le "théorème des milieux) "
ils feraient mieux de s'abstenir, même s'ils pensent avoir la pédagogie infuse; leur intervention est complètement inutile; quant à la relation avec d'autres intervenants qui devrait montrer un respect réciproque, elle devient malsaine.
Ceci dit,PeaceKeeper il reste des choses à expliquer à drumsgirl, parce que j'ai donné une idée mais par exemple faire la figure n'est pas du tout évident et les rotations encore moins.

sans rancune. :we:

[paquito]

Je n'ai en aucun cas fourni une réponse complète! L'élève doit déjà comprendre mes "rotations" ce qui est en fait "hors programme". quand à la solution finale, qui n'est pas du tout évidente, l'élève devra la justifier, ce qui n'est pas évident. Je préconise une figure Géoplan ou Géogébra mais la figure est difficile à faire. J'ai donc donné des indications proportionnelles à la difficulté de l'exercice. Si on comprend ce que j'appelle manipuler le cube, je crois que j'aurais fait travailler sérieusement l'élève (il n'y a rien d'évident).
Quant aux collègues qui répondent:"qu'à tu fait?" ou "pense à thalès";( ici c'est le "théorème des milieux) "
ils feraient mieux de s'abstenir, même s'ils pensent avoir la pédagogie infuse; leur intervention est complètement inutile; quant à la relation avec d'autres intervenants qui devrait montrer un respect réciproque, elle devient malsaine.
Ceci dit,PeaceKeeper il reste des choses à expliquer à drumsgirl, parce que j'ai donné une idée mais par exemple faire la figure n'est pas du tout évident et les rotations encore moins.

sans rancune. :we:

[drumsgirl]

Merci Paquito et Peacekeeper, +paquito +peacekeeper
a vrai dire j'ai la figure sur le sujet mais je ne pouvais pas la mettre (je n'y arrivais pas...)
Désolée si vous vous êtes embêtez avec géogébra... :/

De plus j'ai fais un ds de maths avant les vacances et il y avait cette même figure mais les mêmes questions mais il y avait dans l'énoncé cette phrase : "le solide IJKLMN est un octaèdre régulier (ce qui veut dire que ses faces sont des triangles équilatéraux)".
Donc déjà je connais la réponse pour la question 2 mais comment le démontrer...
j'ai pas très bien compris pour la question 1.....
Par contre une petite question j'ai le droit de me placer dans un triangle qui n'est pas tracer sur la figure ?
Il y avait pas longtemps dans un autre DM, j'avais construis un cercle sur un triangle mais le prof m'a dit qu'il ne fallait pas rajouter des choses même si l'énoncé nous le dit pas...
Donc voila....
Merci beaucoup en tout cas pour vos réponse?
Emma

[drumsgirl]

Je n'ai en aucun cas fourni une réponse complète! L'élève doit déjà comprendre mes "rotations" ce qui est en fait "hors programme". quand à la solution finale, qui n'est pas du tout évidente, l'élève devra la justifier, ce qui n'est pas évident. Je préconise une figure Géoplan ou Géogébra mais la figure est difficile à faire. J'ai donc donné des indications proportionnelles à la difficulté de l'exercice. Si on comprend ce que j'appelle manipuler le cube, je crois que j'aurais fait travailler sérieusement l'élève (il n'y a rien d'évident).
Quant aux collègues qui répondent:"qu'à tu fait?" ou "pense à thalès";( ici c'est le "théorème des milieux) "
ils feraient mieux de s'abstenir, même s'ils pensent avoir la pédagogie infuse; leur intervention est complètement inutile; quant à la relation avec d'autres intervenants qui devrait montrer un respect réciproque, elle devient malsaine.
Ceci dit,PeaceKeeper il reste des choses à expliquer à drumsgirl, parce que j'ai donné une idée mais par exemple faire la figure n'est pas du tout évident et les rotations encore moins.

sans rancune. :we:

Merci Paquito et Peacekeeper,
a vrai dire la figure je l'ai sur le sujet mais je ne pouvais pas la mettre...
Désolée...
j'ai entièrement compris ! Merci beaucoup
Par contre je bloque sur la question 2....

[paquito]

Il faut bien sûr faire la figure qui permet de trouver le résultat, quitte à l'effacer après!
Si l'on trace le triangle FHA (les trois côtés) on a N milieu de HF, L milieu de HA donc d'après le théorème des milieux, on a LN=1/2 AF; or AF est la diagonale d'un carré ce côté 1, donc,
d'où le résultat.

Pour la 2, pour l'instant LN est une arrête de ton octaèdre, mais il en à 12! On ne va pas faire 12 fois la même démonstration!!

Donc, il faut remarquer que toutes les arrêtes sont des segments joignant les centres des faces qui ont un côté en commun et que par conséquent le calcul fait pour LN va être le même pour les 11 autres arrêtes.
Nos 12 arrêtes ont donc la même longueur qui est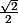 . On peut conclure.

Quant à ton prof, il n'a jamais fait de géométrie!!