Petit problème

[FanMathics]

Bonjour,


J'ai un problème en math que je n'arrive pas à résoudre.
Si quelqu'un pouvait m'aider ce serait gentil.
Mon problème est le suivant: J'ai un cube de 10*10*10 et j'ai aussi 250 parallélépipèdes rectangles de 4*1*1. La question est: Est-il possible de mettre ces 250 pavés droits dans le cube? Si oui donnez un exemple. Si non prouvez que c'est impossible.
(On ne peut bien entendu pas couper les pavés droits).

Mon problème est que j'arrive toujours à mettre 248 pavés droits et puis qu'il me reste un espace de 2*2*2 dans lequel je ne peux plus rien mettre. Mais je n'arrive que à trouver des exemples et je n'arrive pas à prouver cela.

Merci de votre aide.

[Imod]

Bonsoir

Je ne suis pas sûr mais ça ressemble à un problème de coloriage , tu as essayé avec RVBJRVBJ... dans les trois directions ?

Imod

[FanMathics]

Bonsoir

Je ne suis pas sûr mais ça ressemble à un problème de coloriage , tu as essayé avec RVBJRVBJ... dans les trois directions ?

Imod

merci pour la réponse. Je crois avoir trouvé une réponse, mais je la travaillerai demain pcq il commence à se faire tard

[Imod]

En fait ça marche avec le coloriage :

NNBBNNBBNN
NNBBNNBBNN
BBNNBBNNBB
BBNNBBNNBB
NNBBNNBBNN
NNBBNNBBNN
BBNNBBNNBB
BBNNBBNNBB
NNBBNNBBNN
NNBBNNBBNN

Imod

[FanMathics]

Merci de m'avoir aidé. En remplissant tout mon cube avec quatre couleurs je me retrouve dans mon dernier cube de 2*2*2 avec 4 bleus, 2 oranges, 2 rouges et pas de violet

[fatal_error]

hello,

pour moi ce problème se réfère à du 3d bin packing, qui est un problème NP.
Il semble que vous ayez une méthode avec des couleurs ... sauf que je sais pas d'où ca sort..

pouvez-vous me donner quelques mots clés/références?

[Ben314]

C'est une astuce "classique" pour montrer l'impossibilité de paver une surface (ou un volume) donné à l'aide d'un certain type d'objet (ici le problème est de "paver" un cube 10x10x10 avec des barrettes 1x1x4).
L'idée consiste à colorier les cases de l'objet à paver de façon à ce que, où qu'on le place, l'objet "paveur" recouvre toujours les mêmes couleurs. Si l'objet à paver ne contient pas autant de cases de chaque couleur, cela constitue une preuve de l'impossibilité du pavage.

Le cas sans doute le plus connu est :
"Peut-on recouvrir un échiquier 8x8 privé des deux coins diamétralement opposés à l'aide de 31 dominos 1x2"
La réponse est non car chaque domino, où qu'il soit placé recouvre une case blanche et une noire de l'échiquier alors qu'en enlevant les deux coins diamétralement opposés on a enlevé 2 cases de la même couleur.

Pour le 10x10x10, tu fait de même soit avec 4 couleurs, soit uniquement avec 2 en utilisant le motif donné par Imod.
Dans les deux cas tu en déduit l'impossibilité de remplir le cube avec 250 barrettes (tu montre même qu'on en rentre 248 au max)

[fatal_error]

au risque de paraitre lent...

10x10x10==1000 donc divisible par 4 donc à priori c'est possible de paver.
Maintenant est-ce qu'il existe un tel pavage?

dans la solution d'Imod, on est dans le plan avec un 10x12.
Donc déjà je comprends pas pourquoi mettre un 10x12 alors que c'est un 10x10 qui nous intéresse.

Ensuite, en supposant que le 10x10 montre que c'est pas possible de paver (alors que ya bien le même nombre de B et N), je vois pas en quoi ca montre que le 10x10x10 est impossible, parce que
en mettant les dominos à plat, tous prennent 2B2N, mais si on en met deux à la verticale, ben ils prennent que deux cellules.

[Imod]

Il y avait une erreur dans mon dessin : le carré est bien sûr 10X10 :mur:

L'idée est de fabriquer des cubes noirs et des cubes blancs 2X2 . Il y a en tout 504 petits cubes noirs et 496 cubes Blancs . Comme chaque barre 4X1 utilise 2 cubes blancs et deux cubes noirs , il va manquer des blancs pour remplir le grand cube .

Imod

[fatal_error]

haan, smartooos!

j'avais mal compté le nombre de N et B dans le plan... jcroyais qe yavait (N,B)=(50,50) alors que yen avait (52,48)

[FanMathics]

Il y avait une erreur dans mon dessin : le carré est bien sûr 10X10 :mur:

L'idée est de fabriquer des cubes noirs et des cubes blancs 2X2 . Il y a en tout 504 petits cubes noirs et 496 cubes Blancs . Comme chaque barre 4X1 utilise 2 cubes blancs et deux cubes noirs , il va manquer des blancs pour remplir le grand cube .

Imod

Je comprends pas tout à fait ce que tu veux dire pcq si tu commences avec NN à la première rangée tu devrais commencer avec BB à la suivante et donc il y aurait 5 rangées avec un surnombre de noirs et 5 rangées avec un surnombre de blancs ce qui ferait qu'en tout il y aurait autant de blancs que de noirs?

[Imod]

Non , les lignes et colonnes marchent par paires NNBBNNBB... au total il y a donc 8 cubes noirs de plus que de blancs .

Imod

[FanMathics]

Non , les lignes et colonnes marchent par paires NNBBNNBB... au total il y a donc 8 cubes noirs de plus que de blancs .

Imod

Je viens de comprendre merci :we:

[fatal_error]

dans le premier plan tu as
NNBBNNBBNN
NNBBNNBBNN
BBNNBBNNBB
BBNNBBNNBB
NNBBNNBBNN
NNBBNNBBNN
BBNNBBNNBB
BBNNBBNNBB
NNBBNNBBNN
NNBBNNBBNN

dans le plan du dessus: pareil
dans le troisieme plan, tu inverses noir et blanc.
dans le quatrieme, tu copies le troisieme.
si tu regardes de face, tu vois qu'en hauteur tu as soit BBNN soit NNBB

tu copies colles ces 4, ca te fait les plans de 5 à 8
puis tu complètes à 10 en complètant avec les plan 1 et 2

[Ben314]

Au cas où il y en a que ça intéresse, il y a une façon plus "pédante" (i.e. utilisant des maths plus compliquées) de modéliser ces problèmes de coloriages :

A chaque case de coordonnée on associe le monôme .
La somme de tout les monômes du cube vaut donc

D'un autre coté, aux 4 cases de toute barrette 1x1x4 sont associés les 4 monômes de la forme avec dont la somme est
Donc, si on pouvait remplir le cube de barrettes, le polynôme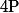 serait somme de tels polynômes et donc divisible par .
Sauf que le complexe est racine de et qu'il n'est pas racine de donc ne divise pas .

Le petit intérêt de la méthode, c'est qu'il permet d'appréhender plus facilement des tailles variables, par exemple on montre de même que, pour qu'on puisse entièrement remplir une grande boite avec des petites boites, il faut que chacune des dimensions des petites boites divisent au moins une des dimensions de la grande boite (et comme 4 ne divise pas 10, cela montre qu'on ne peut pas résoudre le problème de départ).

La méthode (avec coloriage ou polynômes : c'est au fond la même chose) peut aussi servir pour des problèmes plus complexes où elle donne des indications concernant la positions de certaines pièces :
Dans le classique "Comment remplir un cube 5x5x5 à l'aide de 6 boites 2x2x3, de 6 boites 1x2x4 et de 5 cubes 1x1x1" elle donne par exemple des renseignements sur les positions des petits cubes...

[fatal_error]

niiice :zen:

"Comment remplir un cube 5x5x5 à l'aide de 6 boites 2x2x3, de 6 boites 1x2x4 et de 5 cubes 1x1x1" elle donne par exemple des renseignements sur les positions des petits cubes...

vais essayer...

[chan79]

, pour qu'on puisse entièrement remplir une grande boite avec des petites boites, il faut que chacune des dimensions des petites boites divisent au moins une des dimensions de la grande boite (et comme 4 ne divise pas 10, cela montre qu'on ne peut pas résoudre le problème de départ).

Dans le classique "Comment remplir un cube 5x5x5 à l'aide de 6 boites 2x2x3, de 6 boites 1x2x4 et de 5 cubes 1x1x1" elle donne par exemple des renseignements sur les positions des petits cubes...

Salut
Y'a pas une erreur de formulation ? Ca marche avec la boîte 5x5x5 alors que 4 ne divise pas 5.

[Ben314]

Dans "l'exercice classique", l'énoncé, c'est :
Comment remplir un cube 5x5x5 à l'aide de 6 boites 2x2x3 PLUS 6 boites 1x2x4 PLUS 5 cubes 1x1x1.
(comme ça doit remplir entièrement le cube)

Et le théorème
Pour qu'on puisse entièrement remplir une grande boite avec des petites boites, il faut que chacune des dimensions des petites boites divisent au moins une des dimensions de la grande boite
ne s'applique qu'au cas où on doit remplir la grande boite avec des petites boites toutes de la même forme.
Par exemple, ça s'appliquerait si tu te posait la question "peut on entièrement remplir un cube 5x5x5 avec des boites 1x2x4" mais là on a pas besoin du théorème vu que le volume du cube (125) n'est pas divisible par le volume des petites boites (8).

Là où le théorème est pertinent, c'est par exemple sur un "peut-on entièrement remplir un parallélépipède 9x9x8 à l'aide de barrettes 6x1x1".
Là, le volume du parallépipède (9x9x8) est divisible par le volume des barrettes (6) mais la réponse est quand même NON grâce au théorème car 6 ne divise ni 9 ni 8.

[chan79]

OK merci pour la précision

5x5x5 rempli avec six 2x2x3, six 1x2x4 et cinq 1x1x1



Positions des 1x1x1: