Équations symétrique de degré 3
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Jeremy26
- Messages: 6
- Enregistré le: 29 Sep 2014, 18:53
-
 par Jeremy26 » 29 Sep 2014, 18:57
par Jeremy26 » 29 Sep 2014, 18:57
Bonjour, j'ai dans un dm un exo sur les équations symétrique de degré 3 : ax^3 + bx^2 +bx + a = 0 et je dois trouver la solution x0 commune à toutes ces équations et j'ai essayé de faire avec -1 mais je comprends pas trop
Pourriez vous m'aidez ? Merci

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 29 Sep 2014, 19:02
par WillyCagnes » 29 Sep 2014, 19:02
bsr
ax^3 + bx^2 +bx + a = 0
or x0= est solution de cette equation
donc tu peux mettre en facteur (x-x0)
(x-x0)[ax² +px +q] = ax^3 + bx^2 +bx + a = 0
tu developpes le membre de gauche, puis tu identifies p et q
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 29 Sep 2014, 19:03
par siger » 29 Sep 2014, 19:03
bonsoir
utiise la forme symetrique de l'equation..
ecris l'equation sous la forme
a( x^3+1)+ bx(x+1)= 0
.......
-
mathelot
 par mathelot » 29 Sep 2014, 19:07
par mathelot » 29 Sep 2014, 19:07
ah oui, d'accord, il(elle) avait écrit son équation avec des +
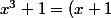(x^2-x+1))
-
Jeremy26
- Messages: 6
- Enregistré le: 29 Sep 2014, 18:53
-
 par Jeremy26 » 29 Sep 2014, 19:12
par Jeremy26 » 29 Sep 2014, 19:12
WillyCagnes a écrit:bsr
ax^3 + bx^2 +bx + a = 0
or x0= est solution de cette equation
donc tu peux mettre en facteur (x-x0)
(x-x0)[ax² +px +q] = ax^3 + bx^2 +bx + a = 0
tu developpes le membre de gauche, puis tu identifies p et q
Je ne comprends pas trop ta méthode avec px et q
-
Jeremy26
- Messages: 6
- Enregistré le: 29 Sep 2014, 18:53
-
 par Jeremy26 » 29 Sep 2014, 19:14
par Jeremy26 » 29 Sep 2014, 19:14
mathelot a écrit:ah oui, d'accord, il(elle) avait écrit son équation avec des +
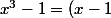(x^2+x+1))
Il faut transposer de l'autre côté ? Parce que ce que tu m'as donné c'est quoi ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Sep 2014, 19:18
par zygomatique » 29 Sep 2014, 19:18
Jeremy26 a écrit:Bonjour, j'ai dans un dm un exo sur les équations symétrique de degré 3 : ax^3 + bx^2 +bx + a = 0 et je dois trouver la solution x0 commune à toutes ces équations et j'ai essayé de faire avec -1 mais je comprends pas trop
Pourriez vous m'aidez ? Merci
salut
bof ...
il suffit d'écrire ::
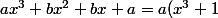 + bx(x + 1))
.... et c'est trivial ....
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 29 Sep 2014, 19:21
par mathelot » 29 Sep 2014, 19:21
hi,hi,hi :we:
-
Jeremy26
- Messages: 6
- Enregistré le: 29 Sep 2014, 18:53
-
 par Jeremy26 » 29 Sep 2014, 19:27
par Jeremy26 » 29 Sep 2014, 19:27
zygomatique a écrit:salut
bof ...
il suffit d'écrire ::
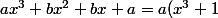 + bx(x + 1))
.... et c'est trivial ....
:zen:
Merci ! J'ai compris c'est pas si compliqué en fait

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 29 Sep 2014, 19:35
par WillyCagnes » 29 Sep 2014, 19:35
L'evidence est trop simple Merci Zygomatique
-
Jeremy26
- Messages: 6
- Enregistré le: 29 Sep 2014, 18:53
-
 par Jeremy26 » 29 Sep 2014, 19:42
par Jeremy26 » 29 Sep 2014, 19:42
Et pour développer (x-x0 )(x^2 +( Beta -1 )x +1 ) ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Sep 2014, 19:45
par zygomatique » 29 Sep 2014, 19:45
quel est le lien avec l'exo ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Jeremy26
- Messages: 6
- Enregistré le: 29 Sep 2014, 18:53
-
 par Jeremy26 » 29 Sep 2014, 19:47
par Jeremy26 » 29 Sep 2014, 19:47
zygomatique a écrit:quel est le lien avec l'exo ?
Montrer que x^3 + beta x^2 +beta x + 1 = à ce que j'ai mis au dessus
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
