Bonjour,
Pouvez-vous me dire si mon exercice est correct.
Énoncé :
On considère pour tout entier naturel supérieur ou égal à 4, le nombre Un défini par Un = 2n² -7n -4
1) Montrer que pour tout entier naturel >= à 4, Un est un entier naturel
2) Montrer que pour tout entier naturel >= à 4, Un est divisible par n-4, puis donner un autre diviseur de Un
Ma réponse :
1)
Un = 2n² -7n -4 avec n>= 4 et Un >=0
Initialisation:
U4 = 2(4)² -7(4) -4 => U4 = 32 - 32 => U4 = 0, la propriété est initialisée au rang 4.
Hérédité:
soit n>=4, on suppose que pour tout entier naturel k tel que 4 =< k =< n , Uk >= 0
Factorisons l'expression 2n² -7n -4 , on obtient (n-4)(2n+1)
Au rang n+1 nous avons :
U(n+1) = ((n+1)-4)(2(n+1)+1) = (n-3)(2n+3), (n-3) et (2n+3) sont >=0 donc la propriété est héreditaire.
Conclusion :
La propriété est vraie au rang 4 et elle est héréditaire, donc pour tout entier naturel n>=4 on a Un >=0.
2)
a)
La factorisation de Un nous donne : Un = (n-4)(2n+1)
(2n+1) est un entier naturel, donc Un est bien divisible par (n-4)
2)
b)
Pour donner un autre diviseur à Un, je cherche la deuxième racine de cette équation.
(je passe l'écriture du discriminant ...)
L'autre diviseur de Un est - 1/2
Arithmétique
10 messages
- Page 1 sur 1
salut
misère de misère ...
 est un trinome du second degré (en n) dont on connaît le signe depuis la première ....
est un trinome du second degré (en n) dont on connaît le signe depuis la première ....
donc nul besoin d'une récurrence qui d'autre part est du grand n'importe quoi ...
si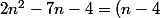(2n + 1)) alors il est trivial que ses diviseurs sont n - 4 et 2n + 1
alors il est trivial que ses diviseurs sont n - 4 et 2n + 1
....
misère de misère ...
donc nul besoin d'une récurrence qui d'autre part est du grand n'importe quoi ...
si
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Tu as 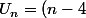(2n+1)) donc il existe bien un entier
donc il existe bien un entier
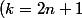) tel que
tel que 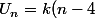) , donc
, donc  est bien divisible par
est bien divisible par 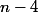 ;
;
Tu as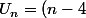(2n+1)) donc il existe bien un entier
donc il existe bien un entier 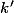
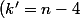) tel que
tel que 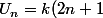) donc
donc  est bien divisible par
est bien divisible par 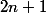 ;
;
Mais tout cela est évident dès que tu as écrit: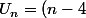(2n+1)) ; si tu écris 6=2x3, tu conclus directement que 6 est divisible par 2 et par 3, non?
; si tu écris 6=2x3, tu conclus directement que 6 est divisible par 2 et par 3, non?
Pour , c'est pareil.
, c'est pareil.
Tu as
Mais tout cela est évident dès que tu as écrit:
Pour
Nabuchodonosor a écrit:Le problème n'est pas la factorisation que je pense avoir assimilé depuis la seconde.
C'est la manière de présenter/répondre à l'exercice.
Puis-je déjà factoriser dans le 1) et si oui, que dire dans le 2) puisqu'il est évident après avoir factorisé que l'expression est divisible par (n-4) !
parce que ton problème est mal posé ... et répondre à 1/ le plus simplement possible consiste à répondre à 2/ en même temps ....
parce que faire une récurrence alors que l'exercice ne s'y prête pas c'est nul ....
vois avec ton prof ce qu'il attend à la question 1/ ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
