Fraction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 08:01
par chatminou » 14 Sep 2014, 08:01
bonjour selon la formule,

et je dois prouver que pour tout entier non nul p
(2p+1)})
=

or d'apres la formule, je ne trouve pas le résultat attendu :
(2p+1)}{p+1*(p+1)(2p+1)} + \dfrac{1*p+1}{(p+1)(2p+1)*p+1})
la je regroupe sous le meme denominateur mais je ne vais pas obtenir le résultat attendu encore une fois
quelqu'un pourrait m'indiquer la marche à suivre car je suis bloqué ?
Merci d'avance

-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 08:14
par Shew » 14 Sep 2014, 08:14
chatminou a écrit:bonjour selon la formule,

et je dois prouver que pour tout entier non nul p
(2p+1)})
=

or d'apres la formule, je ne trouve pas le résultat attendu :
(2p+1)}{p+1*(p+1)(2p+1)} + \dfrac{1*p+1}{(p+1)(2p+1)*p+1})
la je regroupe sous le meme denominateur mais je ne vais pas obtenir le résultat attendu encore une fois
quelqu'un pourrait m'indiquer la marche à suivre car je suis bloqué ?
Merci d'avance

La première fraction a deja comme dénominateur p + 1 on la multiplie à 2p + 1 et on ajoute le tout .
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 08:32
par chatminou » 14 Sep 2014, 08:32
je comprends pas la
peux tu me réexpliquer?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 08:58
par Shew » 14 Sep 2014, 08:58
chatminou a écrit:je comprends pas la
peux tu me réexpliquer?
On a

pour la première et
(2p + 1)})
pour la second, on remarque que

est commun aux deux fractions donc on ramène le tout au même denominateur en multipliant le numérateur et le dénominateur de

par

-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:01
par chatminou » 14 Sep 2014, 09:01
ok donc ca donne 3p+2 et en haut 2p+1 ce qui n'est pas correct ...
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:03
par Shew » 14 Sep 2014, 09:03
chatminou a écrit:ok donc ca donne 3p+2 et en haut 2p+1 ce qui n'est pas correct ...
Pourquoi 3p + 2 au dénominateur ?
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:04
par chatminou » 14 Sep 2014, 09:04
2p + 1 * p+1 = 3p +2
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:07
par Shew » 14 Sep 2014, 09:07
chatminou a écrit:2p + 1 * p+1 = 3p +2
Ah bon ???? Je ne connaissais pas cette règle :ptdr: :ptdr: :ptdr: . En revanche je connais bien 2p + 1
+ p + 1 = 3p + 2 .
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:09
par chatminou » 14 Sep 2014, 09:09
ahhh je suis désolé je confondais :mur: :ptdr:
oui donc tu as bien raison ca donne 2p+1
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:11
par Shew » 14 Sep 2014, 09:11
chatminou a écrit:ahhh je suis désolé je confondais :mur: :ptdr:
oui donc tu as bien raison ca donne 2p+1
Attention
(2p + 1))
au dénominateur :lol3:
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:12
par chatminou » 14 Sep 2014, 09:12
mais pour le numérateur ca donne 2p+1 ? et je dois obtenir 2
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:14
par Shew » 14 Sep 2014, 09:14
chatminou a écrit:mais pour le numérateur ca donne 2p+1 ? et je dois obtenir 2
Maintenant que les deux expressions sont ramenées au même dénominateur vous avez
(2p + 1)} + \frac{1}{(p + 1)(2p + 1)})
, vous pouvez donc calculer entre eux les numérateurs .
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:21
par chatminou » 14 Sep 2014, 09:21
ce qui fait
(2p+1)})
mais je dois obtenir

-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:24
par Shew » 14 Sep 2014, 09:24
chatminou a écrit:ce que fait \dfrac{2p+1}{(p+1)(2p+1)}
mais je dois obtenir \dfrac{2}{2p+1}
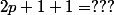
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:25
par chatminou » 14 Sep 2014, 09:25
ca fait 2p + 2 mais pourquoi mets tu ca car je ne peux pas simplifier le denominateur
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:31
par Shew » 14 Sep 2014, 09:31
chatminou a écrit:ca fait 2p + 2 mais pourquoi mets tu ca car je ne peux pas simplifier le denominateur
:hein: :hein: :hein: On a
(2p + 1)} + \frac{1}{(p + 1)(2p + 1)} = \frac{2p + 1 + 1}{(p + 1)(2p + 1)} = \frac{2p + 2}{(p + 1)(2p + 1)})
. Au numérateur mettez 2 en facteur .
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:34
par chatminou » 14 Sep 2014, 09:34
ok mais je ne trouve pas la fraction que je dois normalement trouver
j'ai une idée : je barre le 2p au numérateur et au dénominateur ce qui me fait deux au numérateur et au dénominateur p+2 mais j'obtiens pas 2p+1
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 14 Sep 2014, 09:35
par Shew » 14 Sep 2014, 09:35
chatminou a écrit:ok mais je ne trouve pas la fraction que je dois normalement trouver
j'ai une idée : je barre le 2p au numérateur et au dénominateur ce qui me fait deux au numérateur et au dénominateur p+2 mais j'obtiens pas 2p+1
Je vous ai donné l'astuce mettez 2 en facteur au numerateur .
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:37
par chatminou » 14 Sep 2014, 09:37
je ne vois pas comment vous pouvez mettre 2 en facteur...
-
chatminou
- Membre Naturel
- Messages: 22
- Enregistré le: 11 Sep 2014, 17:06
-
 par chatminou » 14 Sep 2014, 09:41
par chatminou » 14 Sep 2014, 09:41
pourriez vous m'expliquer ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
