Exercice sur les fonctions

[Kamanbiere]

Bonsoir à tous !

Tout d'abord je m'excuse si un manquement aux règles et effectué, j'ai lu la charte, mais un manquement de ma part est possible, donc tout d'abord, je commence par m'excuser

Voilà mon petit problème, après quelques jours de recherche avec des amis, il nous est totalement impossible de trouver une piste, une solution, sur le sujet de maths qui nous a été distribué ...

C'est pour quoi je me présente ici, malheureusement je n'ai pas de piste à vous fournir, malgré mes différents efforts ...

Voici le sujet :
http://i.imgur.com/D0HY7fu.jpg
http://i.imgur.com/ZDmL0kb.jpg


Bien cordialement et merci d'avance

[zygomatique]

salut

la question 1) est la méthode d'Euler ....

[zygomatique]

la méthode d'Euler se trouve sur internet ...

[Cliffe]

On cherche la solution tel que :
[CENTER] [/CENTER]

plutôt que de résoudre directement on veux approchée cette fonction par une fonction linéaire par morceaux (des morceaux de taille ) :

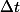
[CENTER] [/CENTER]

Les définissent une suite. On a :


Edit : Je rectifie mon schéma. Les tangentes étaient mal faites et ne montrer les erreurs engendrés par la méthode :
[CENTER]
[/CENTER]

[Kamanbiere]

Je te remerci pour cette réponse qui m'aide grandement, je vais l'étudier, de plus je suis entrain d'essayer de faire le programme qui est demandé.

Si ta des indications pour la suite, j'en serais ravi :)

Cordialement,

Et encore merci pour ton aide Cliffe :lol2:

[Cliffe]

Un truc du genre :

Code: Tout sélectionner

const float a   = ...;
const float b   = ...;
const float D   = ...;
const float M   = ...;
const float y_0 = ...;
const float Dt  = ...;

float f(float x) {
    return ...;
}

int main() {
    float y_n = y_0, y_n_1, nDt = - D / M;
   
    while (nDt <= D / M) {
        nDt += Dt;
        y_n_1 = y_n + f(nDt) * Dt;
    }
}

Tu dois juste afficher un tableau et une courbe.

Pour la Q2 je trouve ça bizarre de prendre un angle initiale égale à 0. Du coup le pendule ne bouge pas non ?

[Kamanbiere]

Théoriquement, l'équa dif est censé régir le mouvement du pendule non ?

[Cliffe]

Théoriquement, l'équa dif est censé régir le mouvement du pendule non ?

Oui, mais si au départ ton pendule à un angle null il ne vas pas bouger oO

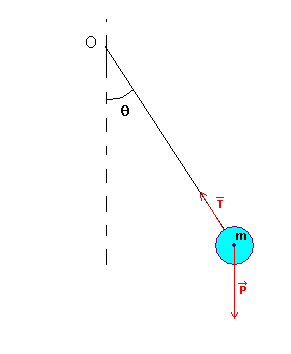
[CENTER][/CENTER]

[Kamanbiere]

De plus, je ne vois absolument pas comment répondre à la question 3 ( n'ayant pas vue Riemman en cours ) ou même répondre à la question 4 .... :(

[Cliffe]

Si un physicien peut m'expliquer l'équation du pendule qui me paraît étrange.

On a :
[CENTER] [/CENTER]

avec la formule : , on obtient :

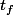
Ici représente la vitesse du pendule pour tout . Or le pendule va changer de sens régulièrement (la vitesse s'annule), donc il existe un tel que : .

Or, on a : .

Avec les valeurs numériques : . Ce qui contredit l'existence de .

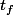
Où est l'erreur ?