Dérivé première et seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
par HERCOLUBUS » 24 Mai 2014, 04:19
Salut à tous !
Je crois que mon corrigé me joue des tours....... :hum:
Je dois trouver la dérivée première et seconde pour analyser la fonction suivante :
=\frac{x^3+1}{x^2-1})
Le corrigé indique que les dérivée première et seconde sont:
=\frac{x(x-2)}{(x-1)^2})
et
=\frac{2}{(x-1)^3})
Je n'arrive jamais à ces résultats, je crois qu'il y a une eurreur dans le corrigé, quelqu'un peut confirmer ? :hein:
Merci !
-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
par capitaine nuggets » 24 Mai 2014, 05:43
salut !
HERCOLUBUS a écrit:Salut à tous !
Je crois que mon corrigé me joue des tours....... :hum:
Je dois trouver la dérivée première et seconde pour analyser la fonction suivante :
Le corrigé indique que les dérivée première et seconde sont:
et
Je n'arrive jamais à ces résultats, je crois qu'il y a une eurreur dans le corrigé, quelqu'un peut confirmer ? :hein:
Merci !
Oui, au premier coup d'oeil, je pensais que c'était faux : le dénominateur a attiré mon attention. En effet, la dérivée de f=u/v est f'=u'v-uv'/v² et là, j'ai un peu de mal à voir, au premier coup d'oeil, où peut bien être le dénominateur (x²-1)² dans f'. Et pourtant, le corrigé est pourtant juste !
Personnellement, je trouve
=\frac{x^4-3x^2-2x}{(x^2-1)^2}=\frac{x(x-2)(x+1)^2}{(x^2-1)^2}=\frac{x(x-2)(x+1)^2}{(x-1)^2(x+1)^2}=\frac{x(x-2)}{(x-1)^2})
et
=\frac{2(x+1)^3}{(x^2-1)^3}=\frac{2(x+1)^3}{(x-1)^3(x+1)^3}=\frac{2}{(x-1)^3})
Rappel : x²-1=(x-1)(x+1) donc (x²-1)²=((x-1)(x+1))²=(x-1)²(x+1)² (même raisonnement pour (x-1)^3 :++:)
:+++:
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
par HERCOLUBUS » 24 Mai 2014, 07:38
capitaine nuggets a écrit:salut !
Oui, au premier coup d'oeil, je pensais que c'était faux : le dénominateur a attiré mon attention. En effet, la dérivée de f=u/v est f'=u'v-uv'/v² et là, j'ai un peu de mal à voir, au premier coup d'oeil, où peut bien être le dénominateur (x²-1)² dans f'. Et pourtant, le corrigé est pourtant juste !
Personnellement, je trouve
et
Rappel : x²-1=(x-1)(x+1) donc (x²-1)²=((x-1)(x+1))²=(x-1)²(x+1)² (même raisonnement pour (x-1)^3 :++:)
:+++:
Pour la première dérivée, tout est réglé ! :id:
Pour ce qui est de la deuxième, je commence a dérivé à partir de cette expression:
=(\frac{(x^2-2x)}{(x-1)^2})'=\frac{(x^2-2x)'(x-1)^2-(x^2-2x)[(x-1)^2]'}{(x-1)^4})
et j'arrive à
=\frac{2(1-x)}{(x-1)^3})
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
par paquito » 24 Mai 2014, 10:37
Tu as rencontré un problème, car quand on calcule f'(x), on trouve au numérateur
)
, et tu n'avais aucune indication pour montrer que
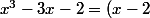(x+1)^2)
.
Pour la dérivée seconde, c'est plus facile la dérivée de (x-1)² étant 2(x-1), tu a une simplification par (x-1) et tu fais tranquillement le calcul qui reste, tout s'élimine et il reste 2.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
