Lemme de topologie

par **algharib** » 10 Mai 2014, 09:04

salut
svp comment démontrer le lemme suivant:

par **ev85** » 10 Mai 2014, 12:20

algharib a écrit:salut
svp comment démontrer le lemme suivant:

Bonjour. Par l'absurde.

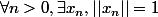
et

. La boule unité est compacte. Son intersection avec un fermé...

ev85

par **adrien69** » 10 Mai 2014, 12:52

Toi tu veux montrer le théorème de Riesz on dirait !

Bon, soit x un élément de E\F,

On pose d=d(x,F), et

Soit y un élément de F tel que

Maintenant, soit v=

Il reste à montrer que v est le bon élément.

Pour tout f dans F,

car F est un sev de E,

Et donc pour tout f dans F,

Le numérateur étant supérieur à d (car la distance de x à F vaut d) et le numérateur inférieur à

par définition de y,

v est bien ce qu'on cherchait.

par **adrien69** » 10 Mai 2014, 12:54

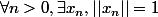
ev85 a écrit:Bonjour. Par l'absurde. et . La boule unité est compacte. Son intersection avec un fermé...

ev85

FAUUUUX ! On n'est pas nécessairement en dimension finie ! C'est même tout le contraire vu que c'est un lemme du théorème de Riesz (la boule unité est compacte ssi on est en dimension finie) !

par **ev85** » 10 Mai 2014, 13:23

adrien69 a écrit:FAUUUUX ! On n'est pas nécessairement en dimension finie ! C'est même tout le contraire vu que c'est un lemme du théorème de Riesz (la boule unité est compacte ssi on est en dimension finie) !

Raaaah ! Comme je suis en week-end, je me suis cru en dimension finie !

e.v.

par **adrien69** » 10 Mai 2014, 14:48

Grand classique !

par **algharib** » 11 Mai 2014, 17:12

adrien69 a écrit:Toi tu veux montrer le théorème de Riesz on dirait !

Bon, soit x un élément de E\F,

On pose d=d(x,F), et

Soit y un élément de F tel que

Maintenant, soit v=

Il reste à montrer que v est le bon élément.

Pour tout f dans F,

car F est un sev de E,

Et donc pour tout f dans F,

Le numérateur étant supérieur à d (car la distance de x à F vaut d) et le numérateur inférieur à par définition de y,

v est bien ce qu'on cherchait.

Merci, mais où utilisé le fait que F fermé

par **jlb** » 11 Mai 2014, 17:30

salut: existence de y : d(x,F)=0 équivaut à x appartient à l'adhérence de F

par **jlb** » 11 Mai 2014, 17:35

salut, pour justifier que d est différent de 0 ( E=[1,2] et F=]1,2[ , si F pas fermé, pb)

le truc c'est que d(x,F)=0 équivaut à x appartient à l'adhérence de F.

par **jlb** » 11 Mai 2014, 17:42

Salut explique pourquoi d est différent de 0 sinon cela va être délicat d'exhiber ce y!!!

par **adrien69** » 11 Mai 2014, 18:56

d(x,F)>0 parce que F est fermé.

Lemme de topologie

Lemme de topologie

Qui est en ligne