ABCD est un carré de coté l
E est le milieu de [AB]
Le cercle C de centre E pasant par C et coupe [AB] en F
On construit le rectangle AFGD
1) On souhaite démontrer que AF = lx(1+racine carrée de 5) tout sa /2
a) Montrer que AF = AE+ EF
b) Montrer que EC = EF
c) Appliquer le théorème de pythagore dans le triangle EBC rectangle en B puis exprimer EC en fonction de l .
Voici mon problème j'espére que vous pourrez m'aider =/
Nombre d'or / rectangle
11 messages
- Page 1 sur 1
Bon on va dire que c'est "coupe (AB) en F" et que G est le point sur (DC) tel que (FG) // (BC).
Je ne vois pas ce que ça pourrait être d'autre !
On a donc quelque chose comme
A_E_B_F
|
D___C_G
D'après l'énoncé) donc A, B, F sont alignés. D'après le théorème de Chasles
donc A, B, F sont alignés. D'après le théorème de Chasles
AF = AE + EB
D'après l'énoncé C et F sont sur le cercle avec E son centre, le rayon du cercle est donc EC = EF.
Dans EBC, d'après le théorème de Pythagore
EC² = EB² + BC²
EC² =^2) +
+ 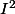
EC =
EC =
EC =
Au passage on voit qu'on a toujours EC > I > EB, F ne peut pas être sur [AB].
Je ne vois pas ce que ça pourrait être d'autre !
On a donc quelque chose comme
A_E_B_F
|
D___C_G
D'après l'énoncé
AF = AE + EB
D'après l'énoncé C et F sont sur le cercle avec E son centre, le rayon du cercle est donc EC = EF.
Dans EBC, d'après le théorème de Pythagore
EC² = EB² + BC²
EC² =
EC =
EC =
EC =
Au passage on voit qu'on a toujours EC > I > EB, F ne peut pas être sur [AB].
kelthuzad a écrit:Bon on va dire que c'est "coupe (AB) en F" et que G est le point sur (DC) tel que (FG) // (BC).
Je ne vois pas ce que ça pourrait être d'autre !
On a donc quelque chose comme
A_E_B_F
|
D___C_G
D'après l'énoncédonc A, B, F sont alignés. D'après le théorème de Chasles
AF = AE + EB
D'après l'énoncé C et F sont sur le cercle avec E son centre, le rayon du cercle est donc EC = EF.
Dans EBC, d'après le théorème de Pythagore
EC² = EB² + BC²
EC² =+
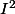
EC =
EC =
EC =
Au passage on voit qu'on a toujours EC > I > EB, F ne peut pas être sur [AB].
Merci beaucoup tu m'a étais d'une grande aide par contre si tu pouvais m'éclairer sur le théorème de Chasles car je ne l'ai pas vu en cours ..
J'ai fait les calculs en "lisant" C coupe (AB) en F (c'est sûr qu'il ne peut pas couper [AB]) et en cherchant AF sans même relire l'énoncé, mais je suis sûr que c'était le but de l'exercice, même si l'énoncé est troublant. C'est un exercice ultra classique pour définir le nombre d'or et le rectangle d'or.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
