Bonjour,
est-que quelq'un peut m'aider a factoriser le polynome suivant :
x³-3x²+4
le resultat qu'on doit obtenir est : (x+1) (x-2)au carre
Merci beaucoup!
Aide avec ce polynome du 3e degre
6 messages
- Page 1 sur 1
Bump of Chicken a écrit:Bonjour,
est-que quelq'un peut m'aider a factoriser le polynome suivant :
x³-3x²+4
le resultat qu'on doit obtenir est : (x+1) (x-2)au carre
Merci beaucoup!
Salut,
Il y a plusieurs façons de traiter cette questions:
Le nombre
On en déduit que
Remarque que tu obtiens une identité remarquable donc
Al-Kashi a écrit:Salut,
Il y a plusieurs façons de traiter cette questions:
Le nombreest une racine évidente car
donc on peut factoriser par
. On écrit donc:
. Après développement et identification on trouve
.
On en déduit que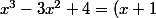(x^2-4x+4))
Remarque que tu obtiens une identité remarquable donc
Merci beaucoup!
Est-ce que tu me peut donner peut etre une site etc. ou cette methode est expliquee en detail?
La meilleure méthode (et la seule niveau lycée) est de chercher une solution "évidente" et de factoriser. On peut chercher des solutions entières parmi les diviseurs du terme constant, ici 4. Les solutions entières, s'il y en a, appartiennent nécessairement à l'ensemble {1;-1;2;-2;4;-4} puisque x(x²-3x)=-4
Sinon, on peut bidouiller, même si c'est sans grand intérêt:
x³-3x²+4=x²(x-3)-(x-3)+(x+1)=(x-3)(x²-1)+(x+1)
=(x-3)(x-1)(x+1)+(x+1)=(x+1)((x-3)(x-1)+1)=(x+1)(x²-4x+4)=(x+1)(x-2)²
Sinon, on peut bidouiller, même si c'est sans grand intérêt:
x³-3x²+4=x²(x-3)-(x-3)+(x+1)=(x-3)(x²-1)+(x+1)
=(x-3)(x-1)(x+1)+(x+1)=(x+1)((x-3)(x-1)+1)=(x+1)(x²-4x+4)=(x+1)(x-2)²
Autres possibilités :
On calcule
On retranche alors ce résultat du polynôme (cela ne change rien puisque c'est 0)
+4-4=0\\ou\\x^3-2^3-3(x^2-2^2)=0\end{array})
On termine en utilisant les identités remarquables :
(x^2+2x+2^2)-3(x-2)(x+2)\\ou\\(x-2)(x^2+2x+4-3x-6)\end{array})
c'est à dire,
(x-2)(x²-x-2) ou encore (x-2)(x+1)(x-2)
On peut également utiliser la méthode de Horner (hors programme au Lycée, même si dans un passé pas si lointain on l'enseignait).
Elle est détaillée ici par ex :
http://integraledesmaths.free.fr/idm/EquMetHor.htm
On calcule
On retranche alors ce résultat du polynôme (cela ne change rien puisque c'est 0)
On termine en utilisant les identités remarquables :
c'est à dire,
(x-2)(x²-x-2) ou encore (x-2)(x+1)(x-2)
On peut également utiliser la méthode de Horner (hors programme au Lycée, même si dans un passé pas si lointain on l'enseignait).
Elle est détaillée ici par ex :
http://integraledesmaths.free.fr/idm/EquMetHor.htm
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 169 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
