Expression d'un produit grace aux complexes

[chnafon]

Bonsoir.

Je me trouve confronté au problème suivant, en deux étapes.

1/ dans C, effectuer la décomposition en éléments simple de X^(2n) - 1.

J'arrive à X^(2n) - 1 = produit(X-exp(k;)/n))(X+exp(k;)/n)), k allant de 1 à n. Une décomposition assez classique, je crois avoir juste. (On recherche U = X² les racines n-ième de l'unité...)

2/ en déduire l'égalité suivante: http://www.noelshack.com/2014-16-1397493858-captured.jpg

Mon problème se situe au niveau de la question 2/, je n'ai pas du tout d'idée. J'ai pensé a utilisé l'expression classique P'/P, ou encore tenter de bidouiller avec les parties réelles et imaginaires, rien n'y fait. Peut-être remarquer que l'expression dans le produit est égale à (a-cos(k;)/n))² + sin²(k;)/n) ? Bref, je m'en remets à vous avec ma gratitude d'avance.

[wserdx]

Il doit te manquer un "i" dans tes exponentielles. Et les signes ne sont pas au bon endroit.
Développe le produit correspondant aux racines conjuguées.

[Ben314]

Salut,
Les racines (simples) du polynôme sont les racines -ièmes de l'unité, c'est à dire les où donc (car le polynôme est unitaire).

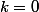Si on considère "à part" les deux racines réelles et (correspondant à et 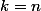) et qu'on regroupe les autres qui sont 2 à 2 conjuguées, on obtient .

En développant les termes correspondant à des racines conjuguées on obtient la décomposition en facteurs irréductibles sur , à savoir : .

Ensuite, faire attention au fait que le produit demandé va de k=1 à n et pas de k=1 à n-1...