Bonjour je cherche à tracé une fonction un peu inhabituelle :
Je voudrais obtenir l'angle T (en réalité Theta ...) en fonction de l'angle a (alpha) :
La relation entre les 2 étant :
(h*cos(a)-d*cos(T)+l)^2 + (-h*sin(a)+d*sin(T)+q)^2 = L^2
Avec h = 5.50 mm
L = 70 mm
q= 67.5 mm
d = 17.9 mm
l = 20.97 mm
Au vu de la relation qui n'est pas du type y=f(x) je n'arrive tous bonnement pas à tracer la courbe ....
Merci d'avance pour votre aide.
Tracé de fonction
13 messages
- Page 1 sur 1
Salut,
Ton truc :^2+ (-h\sin\alpha+d\sin\theta+q)^2 = L^2)
C'est clairement un problème de "tiges articulées" où en fait tu cherche tout les quadrilatères de longueurs de coté fixées.
Si tu veut en fonction de
en fonction de  (avec le reste connu), tu écrit :
(avec le reste connu), tu écrit :
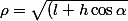^2+(q-h\sin\alpha)^2}\) et
et )
(qui sont des fonctions de ) de façon à avoir
) de façon à avoir
 et
et 
et à ce qsue ton équation s'écrive plus simplement :
^2+ (\rho\sin\varphi+d\sin\theta)^2 = L^2)
qui en la développant donne :
=L^2-\rho^2-d^2)
soit encore
=\frac{\rho^2+d^2-L^2}{2d\rho})
C'est à dire
) à condition évidement que
à condition évidement que 
Il y a évidement deux solutions selon que l'articulation correspondante est "rentrante" dans le quadrilatère ou "sortante"
Ton truc :
C'est clairement un problème de "tiges articulées" où en fait tu cherche tout les quadrilatères de longueurs de coté fixées.
Si tu veut
(qui sont des fonctions de
et à ce qsue ton équation s'écrive plus simplement :
qui en la développant donne :
soit encore
C'est à dire
Il y a évidement deux solutions selon que l'articulation correspondante est "rentrante" dans le quadrilatère ou "sortante"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bizarre : Je viens de relire deux fois les calculs et je ne trouve pas d'erreur.
A la rigueur, en constatant que dans ton problème et donc que
dans ton problème et donc que  pour tout
pour tout  , on peut directement prendre
, on peut directement prendre ) au lieu de passer par l'arc moitié, mais ça ne change absolument rien à la suite...
au lieu de passer par l'arc moitié, mais ça ne change absolument rien à la suite...
Edit : je viens de vérifier avec géogébra : ça me donne bien ce qu'il faut (à moins d'un milième de degré prés...)

A la rigueur, en constatant que
Edit : je viens de vérifier avec géogébra : ça me donne bien ce qu'il faut (à moins d'un milième de degré prés...)

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
A excuse moi pour le phi, j'ai justement prit celui que tu viens de me donner, je n'arrivais pas à retomber sur celui de ton premier message ^^'
Par modélisation des liaisons pivots sur solidworks j'ai un débattement angulaire de -20.5° et de 15.2 °. En théorie il mène exactement le même calcul que celui réalisé à la main et pourtant en traçant la courbe je tombe sur -9.9° et 26°. Je vais la retracer pour vérifié qu'il n'y a pas une erreur dans ce que j'ai rentré.
Et expérimentalement on tombe à -17° et 19°
P.S : je n'arrive pas à lire les valeurs sur ta photo donc je n'est pas comparé avec les miennes.
Par modélisation des liaisons pivots sur solidworks j'ai un débattement angulaire de -20.5° et de 15.2 °. En théorie il mène exactement le même calcul que celui réalisé à la main et pourtant en traçant la courbe je tombe sur -9.9° et 26°. Je vais la retracer pour vérifié qu'il n'y a pas une erreur dans ce que j'ai rentré.
Et expérimentalement on tombe à -17° et 19°
P.S : je n'arrive pas à lire les valeurs sur ta photo donc je n'est pas comparé avec les miennes.
Ça ne m'étonne pas, l'autre correspond à un quadrilatère "croisé" qui a peu de chance de correspondre à un "vrai" système physique...Nabreus a écrit:J'ai bien évidemment prit la solution avec + arccors car celle avec - donnait quelque chose d'impossible par rapport au système que j'étudie.
Pour la photo, c'est pas terrible, mais là, c'est à peu prés lisible :

En fait, j'ai pris alpha=68.3061° et ça me donne theta=24.0444° (que ce soit par le calcul ou en traçant le quadrilatère)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui donc sa correspond avec la courbe que j'ai mit (première coordonnée : alpha en rad, 2e coordonnée theta en °).
La seul bizarerie c'est que bien que le débattement angulaire total (crète à crète) correspondent toujours entre mes différents résultat, on a un plateau qui penche de 15 ° de plus d'un coté que l'autre avec cette solution ...
Sur le système réel l'écart n'est que de 2 ° entre le débattement d'un coté et celui de l'autre.
Enfin bon, c'est pas bien grave ^^ sa me fait quelque chose à raconter pour cette expo.
En tous cas merci beaucoup de ton aide !
La seul bizarerie c'est que bien que le débattement angulaire total (crète à crète) correspondent toujours entre mes différents résultat, on a un plateau qui penche de 15 ° de plus d'un coté que l'autre avec cette solution ...
Sur le système réel l'écart n'est que de 2 ° entre le débattement d'un coté et celui de l'autre.
Enfin bon, c'est pas bien grave ^^ sa me fait quelque chose à raconter pour cette expo.
En tous cas merci beaucoup de ton aide !
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

