Alors voilà, j'ai un DM à rendre pour lundi, contenant deux exercices ( je ferai un autre topic pour l'autre exercice, car il n'a rien à voir avec les vecteurs ), j'ai longtemps cherché, je pense trouver une piste, mais j'aurais besoin d'aide pour les calculs
Voici l'énoncé:
Soit un triangle ABC
Soit les points M et N, tel que : vecteur AM = 1/3 AB et vecteur AN = 1/3 AC
I est le milieu du segment [MN] et J est le milieu du segment [BC]
Que peut-on dire des points A, I et J
Alors je sais pas trop si ça pourra vous aider, j'ai essayé de trouver un schéma se rapprochant du même que sur mon exercice
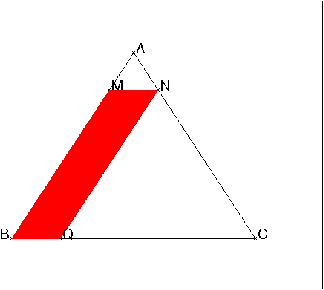
Donc sur le schéma de mon exercice, il y a quelques différences: Le point " Q" juste à droite de B n'existe pas, il n'y a pas non plus le surligneur rouge, et I est le milieu de MN, et J est le milieu de BC, en espérant que cela vous aide à visualiser
Donc pour cette question, je pense bien sûr que A, I, J sont alignés.
Pour cela il faudrait montrer que AI et AJ sont colinéaires non ?
Donc que le vecteur AJ = k x le vecteur AI.
Donc ça je pense que c'est juste.
Donc il faut calculer les vecteurs AI et AJ
AI= AM+MI
MI= 1/2 BJ et MN= MA+AN ( relation de Chales, MA+AN= MN)
Donc AI= 1/3 AB + 1/2 BJ ???
Et donc AJ= AB+BJ
AJ= AB+ 1/2 BC
AJ= 3/3 AB + 1/2 BC
Ces calculs là sont justes ?
Et si oui, comment détermine le réel k ?
Merci pour votre aide
