Relation d'ordre

[estellepierre]

Bonjour,
J'ai un DM (et oui à la fac c'est toujours possible ;)) à rendre dans 1 semaine, ça fait déjà une semaine que j'y travaille mais je dois avouer que là je bloque...

Voici l'intitulé de la question sur laquelle j'ai du mal :
"Soit un ensemble E, bien ordonné et ne possédant pas d'élément maximal. Démontrer que l'ensemble des majorants d'un élément x de E, qui sont différents de x, possède un plus petit élément. On le note s(x) et on le nomme le successeur de x. Démontrer que l'application s qui associe s(x) à x est injective. Est-elle surjective ?
Que peut-on dire de E si l'image de E par s est E privé d'un élément ?"

Voilà voilà merci d'avance pour vos réponses !

[Ben314]

Salut,
- Si tu cherche la définition dans ton cours de "bien ordonné", ça te donne quasi directement la réponse à la première question (existence de s(x)).
- Toujours en regardant la définition de "bien ordonné" et en voyant que cela implique "totalement ordonné", ça te vend que, si x est différent de y alors x- Concernant la surjectivité, il te suffit de prendre comme exemple le plus connu des ensembles qui muni de la relation d'ordre usuelle est bien ordonné.
- "Que peut-on dire de E si l'image de E pas s est privé d'un élément ?" je comprend pas la phrase.

[estellepierre]

Salut,
- Si tu cherche la définition dans ton cours de "bien ordonné", ça te donne quasi directement la réponse à la première question (existence de s(x)).
- Toujours en regardant la définition de "bien ordonné" et en voyant que cela implique "totalement ordonné", ça te vend que, si x est différent de y alors x<y (ou le contraire) et on montre façilemen que ça implique s(x)<s(y) (ou le contraire) : donc c'est plié en ce qui concerne l'injectivité.
- Concernant la surjectivité, il te suffit de prendre comme exemple le plus connu des ensembles qui muni de la relation d'ordre usuelle est bien ordonné.
- "Que peut-on dire de E si l'image de E pas s est privé d'un élément ?" je comprend pas la phrase.

Merci beaucoup pour ta réponse ! Je n'ai pas eu de cours sur cette partie là des relations d'ordre, et ce DM en fait office...
Pour les deux premiers points, il n'y a pas de soucis j'ai bien compris tes explications, cependant pour la surjectivité j'ai un peu de mal à te suivre.
Pour le dernier point je voulais mettre "Que peut-on dire de E si l'image de E par s est E privé d'un élément ?" Désolée pour les petits oublis.

[Ben314]

Pour être un peu plus précis :
- "bien ordonné", ça veut dire en particulier que toute partie non vide admet un plus petit élément donc pour justifier que s(x) existe, il suffit de montrer que tout x admet au moins un majorant strict ce qui est clair vu que E n'a pas de plus grand élément (dans un ensemble totalement ordonné un élément sans majorant strict est forcément le plus grand élément de l'ensemble)
- Si x- L'exemple "de base" d'ensemble totalement ordonné, c'est N (évidement muni de la relation d'ordre usuelle".
Tout élément de N est-il le successeur d'un autre élément de N (<=> la fonction succeseur est-elle surjective)
Et dans le cas d'un ensemble bien ordonné quelconque ?
- Si l'image de E par s est E privé d'un élément xo alors on peut montrer que E est isomorphe (au sens des ensembles ordonnés) à N. Pour ce faire, tu considère l'application qui, à l'entier n de N, associe f(n)=s(s(s...(s(xo))...))) où tu prend n fois la fonction s et tu montre que f est une bijection croissante.

[estellepierre]

Eh bien merci, c'est beaucoup plus clair !

J'avais une autre question pour laquelle j'ai eu du mal : "L'ensemble (0,1)* ordonné par l'ordre lexicographique est-il bien ordonné ?"
J'ai réussi à comprendre pour l'ensemble N*N mais avec l'ensemble (0,1)* j'ai du mal.

[Ben314]

Je sais pas trop ce que désigne "l'ensemble (0,1)*".
Vu le contexte, je suppose que c'est les "mots" de longueur quelconque que l'on peut écrire avec les "lettres" 0 et 1 (et que l'on ordonne à l'aide de l'ordre lexicographique).
Si c'est bien ça, il me semble qu'il est effectivement bien ordonné mais que ce n'est pas complètement évident à démontrer...

[Ben314]

Non, en fait, l'ensemble des "mots" de longueur quelconque n'est pas bien ordonné (il faut limiter la taille si on veut que ça marche) :
L'ensemble des mots {1,01,001,0001,00001,...} n'a pas de plus petit élément.

[estellepierre]

Oui il me semble que c'est bien les mots de longueur quelconque.
En complément à cette question ma prof nous avait donné cet indice (qui je l'avoue ne m'aide pas trop) : "Soient m1 et m2 deux mots, si m1 est un préfixe de m2, alors m1<=m2
sinon, m1 et m2 sont différents de "epsilone" et on peut les écrire :
m1 = m0a1m1'
m2 = m0a2m2 où a1 différent de a2, a1 et a2 appartiennent à (0,1), m0, m1' et m2' peuvent être vides.

m1m2"

[Ben314]

Oui il me semble que c'est bien les mots de longueur quelconque.
En complément à cette question ma prof nous avait donné cet indice (qui je l'avoue ne m'aide pas trop) : "Soient m1 et m2 deux mots, si m1 est un préfixe de m2, alors m1m2"

Pour moi, c'est pas trop un "indice" ton truc : il me semble que c'est juste la définition de l'ordre lexicographique...

[estellepierre]

Bonsoir !

Un petite question en plus pour laquelle je ne suis pas sûre...

"Donnez un exemple d'ensemble bien ordonné qui admet un plus grand élément, et un qui n'en admet pas."
Est ce que si pour la première partie je mets l'intervalle fermé (1;100) et pour la deuxième partie l'intervalle ouvert (1;100( cela fonctionne ?

[Ben314]

Bonsoir !

Un petite question en plus pour laquelle je ne suis pas sûre...

"Donnez un exemple d'ensemble bien ordonné qui admet un plus grand élément, et un qui n'en admet pas."
Est ce que si pour la première partie je mets l'intervalle fermé (1;100) et pour la deuxième partie l'intervalle ouvert (1;100( cela fonctionne ?

Vu le contexte, ç'est pas clair tes réponse, mais de toute façon, ça marche pas...

CAS I : tes intervalles désignent les entiers compris entre tant et tant.
Dans ce cas (1,100)={1,2,3,...,99,100} est bien un ensemble bien ordonné (pour l'ordre usuel) admettant un plus grand élément (qui est 100), sauf que (1,100(={1,2,3,...,99} et lui aussi un ensemble bien ordonné admettant un plus grand élément (qui est 99).

CAS II : tes intervalles désignent les réels compris entre tant et tant.
Dans ce cas (1,100) n'est pas un ensemble bien ordonné (pour l'ordre usuel) : la partie )0,1( de (0,100) est non vide mais n'admet pas de plus petit élément.

Résumé : tu as bien trouvé un ensemble bien ordonné avec un plus grand élément, mais tu n'en a pas trouve de "sans plus grand élément".

[jonses]

"Donnez un exemple d'ensemble bien ordonné qui admet un plus grand élément, et un qui n'en admet pas."

L'ensemble des entiers naturels ? ça peut peut-être faire l'affaire pour "ensemble bien ordonné sans plus grand élément", non ?

[Ben314]

ça peut... et c'est même de loin l'exemple le plus simple... : en trouver un autre n'est pas complètement évident...

Et si tu veut fair vicieux pour l'ensemble bien ordonné AVEC plus grand élément, tu peut prendre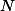 auquel tu ajoute un nouvel élément que l'on va noter par exemple et tu muni ton nouvel ensemble d'une relation d'ordre en prenant la relation usuelle entre deux entiers et en rajoutant la définition pour tout entier .
Clairement cet ensemble admet un plus grand élément, mais il reste à vérifier que la relation sur cet ensemble est bien une relation d'ordre et qu'elle définie un bon ordre (pas dur du tout, mais il faut l'écrire)

[jonses]

Et si tu veut faire vicieux pour l'ensemble bien ordonné AVEC plus grand élément, tu peut prendre auquel tu ajoute un nouvel élément que l'on va noter par exemple et tu muni ton nouvel ensemble d'une relation d'ordre en prenant la relation usuelle entre deux entiers et en rajoutant la définition pour tout entier .
Clairement cet ensemble admet un plus grand élément, mais il reste à vérifier que la relation sur cet ensemble est bien une relation d'ordre et qu'elle définie un bon ordre (pas dur du tout, mais il faut l'écrire)

Bien vu pour l'ensemble "bien ordonné avec un plus grand élément" :++:
Je trouve qu'elle a de la classe

[Ben314]

En fait, il y a toute une théorie concernant la classe des ensembles bien ordonnés qu'on appelle la classe des "ordinaux" (cherche sur ton moteur de recherche préféré)

[jonses]

En fait, il y a toute une théorie concernant la classe des ensembles bien ordonnés qu'on appelle la classe des "ordinaux" (cherche sur ton moteur de recherche préféré)

Merci ! Je vais voir ça !

[estellepierre]

Merci pour vos réponses et votre aide !