Arithmétique calcule de pgcd et ppcm
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
 par mu4l » 02 Mar 2014, 15:48
par mu4l » 02 Mar 2014, 15:48
Bonjour,
Je dois calculer le pgcd et ppcm de :

et

J'ai commencé en essayant de réduire comme cela :
 = pgcd ((12x^2 + 16x + 4) -4x(3x + 3), 3x + 3))
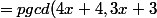 = pgcd( x + 1, 3(x+1)))
Je voudrais savoir si les calcule sont bon est que dois-je faire pour terminer l'exercice.
Merci d'avance pour vos réponse.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 16:06
par adrien69 » 02 Mar 2014, 16:06
Les calculs sont exacts. Et maintenant, pgcd (x+1,3(x+1)) tu ne sais pas dire directement ce que c'est ?
pgcd = plus grand diviseur commun.
Quel est le plus grand diviseur commun polynomial (et unitaire) de x+1 et de 3(x+1) ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 16:07
par adrien69 » 02 Mar 2014, 16:07
Et puis tu t'es franchement cassé la tête pour rien, mais je t'expliquerai ça après.
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
 par mu4l » 02 Mar 2014, 16:35
par mu4l » 02 Mar 2014, 16:35
Merci pour ta réponse, donc le PGCD et donc x+1 ?
Si c'est le cas alors pour calculer le PPCM je dois faire :
 = \frac{(12x^2 + 16x + 4)*(3x + 3)}{x+1})
}{x + 1})
Bon la je suis de nouveau coincé... J'ai du encore choisir la méthode la plus dure :mur:
Et je serait franchement intéressé si il y a une méthode plus rapide

-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 17:28
par adrien69 » 02 Mar 2014, 17:28
Mais quelle idée de développer ton produit ! Tu peux pas faire (3x+3)/(x+1) ?
Comme ça le PPCM c'est 3(12x²+6x+4) et puis basta (modulo une constante multiplicative).
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 17:31
par adrien69 » 02 Mar 2014, 17:31
Bon sinon, comment être malin ?
Quand tu décomposes tes polynômes en facteurs irréductibles,


, comment repère-t-on le PGCD et le PPCM (astuce, c'est comme dans

)
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
 par mu4l » 02 Mar 2014, 17:54
par mu4l » 02 Mar 2014, 17:54
Euhhh, je pense que j'ai pas compris cette méthode.
Sinon la ce comprend pas pour quoi le PPCM c'est 3(12x²+6x+4)
Car

-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 17:55
par adrien69 » 02 Mar 2014, 17:55
 = \frac{(12x^2 + 16x + 4)*(3x + 3)}{x+1} =(12x^2 + 16x + 4)*\frac{(3x + 3)}{(x+1)})
voilà pourquoi.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 17:59
par adrien69 » 02 Mar 2014, 17:59
Pour le reste, imaginons qu'on te demande de calculer le pgcd de 3*7*11²*13 et de 2*3²*11*17, comment tu fais ?
Généralisons.
Si on te demande le pgcd de
(x+1)(x-1)²(x+1.2) et de x(x-1)(x+2), comment tu fais ?
Si c'est le PGCD de (x+1)(12x+4) et de 3x+3, comment tu fais ?
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
 par mu4l » 02 Mar 2014, 18:29
par mu4l » 02 Mar 2014, 18:29
Merci pour le détail.
Pour calculer de 3*7*11²*13 et de 2*3²*11*17
déjà de calcule la somme des deux valeur puis j'utilise l'algorithme d'euclide et je trouve 33.
Je suppose que l'on peut aussi déterminer le pgcd en multipliant les valeurs communes ici 3 et 11 qui font bien 33.
Pour (x+1)(x-1)²(x+1.2) et de x(x-1)(x+2) malheureusement je ne vois pas.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 18:35
par adrien69 » 02 Mar 2014, 18:35
C'est simple c'est pareil.
Mais tu ne connais que l'algorithme d'euclide pour calculer un pgcd ? Auquel cas il vaudrait mieux que je ne t'embête pas avec ça.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 02 Mar 2014, 18:39
par adrien69 » 02 Mar 2014, 18:39
Quand est-ce qu'on dit qu'un polynôme P à coefficients dans R divise un polynôme Q à coefficients dans R aussi ?
Quand les racines complexes de P sont aussi des racines de Q et que leur multiplicité est inférieure dans P que dans Q.
-
mu4l
- Messages: 7
- Enregistré le: 04 Avr 2012, 20:47
-
 par mu4l » 02 Mar 2014, 19:15
par mu4l » 02 Mar 2014, 19:15
Je crois que je vais laissé tomber la méthode courte pour le moment car j'ai du mal à suivre.
Merci pour les réponses.
-
bneay
- Membre Naturel
- Messages: 53
- Enregistré le: 06 Jan 2014, 23:04
-
 par bneay » 03 Mar 2014, 17:34
par bneay » 03 Mar 2014, 17:34
adrien69 a écrit: = \frac{(12x^2 + 16x + 4)*(3x + 3)}{x+1} =(12x^2 + 16x + 4)*\frac{(3x + 3)}{(x+1)})
voilà pourquoi.
attention! le ppcm est unitaire, faut diviser par le dominant!
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 03 Mar 2014, 17:41
par adrien69 » 03 Mar 2014, 17:41
Je considère personnellement que le ppcm est une classe de polynômes, et donc en prendre un représentant ça ne change rien à mes yeux.
Mais si ça peut te faire plaisir regarde ce que j'ai écrit un peu avant :
modulo une constante multiplicative
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités