Pgcd et ppcm
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 02 Mar 2008, 18:03
par legeniedesalpages » 02 Mar 2008, 18:03
Bonjour,
je galère à prouver quelques propriétés élémentaires:
Soient
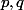
deux entiers positifs non nuls, on définit leurs diviseurs communs et leurs multiples communs:
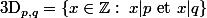
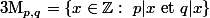
leur pgcd et leur ppcm:
=\max\ D_{p,q}\cap (\mathbb{N}\setminus \{0\}))
=\min\ M_{p,q}\cap (\mathbb{N}\setminus \{0\}))
.
Comment montrer que
Pour tout
)
,
Pour tout
|x)
.
Merci pour votre aide.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 02 Mar 2008, 18:22
par raito123 » 02 Mar 2008, 18:22
pgcd(p,q)=d => il y au moins un U et V dans Z² tel que pU+qV=d
x|p et x|q donc x|pU et x|qV donc x|pU+qV alors x|d donc x|pgcd(p,q)
Les multiples ne doivent pas être utilisés sans nécessité
 par legeniedesalpages » 02 Mar 2008, 18:37
par legeniedesalpages » 02 Mar 2008, 18:37
ah oui c'est vrai qu'on peut y aller à coup de Bezout pour le pgcd, et pour le ppcm tu as une idée?
 par alavacommejetepousse » 02 Mar 2008, 18:48
par alavacommejetepousse » 02 Mar 2008, 18:48
bonsoir
l'ensemble des multiples (relatifs)de p est le sous groupe engendré par p
l'ensemble des multiples communs de p et q est l'intersection des deux sous groupes c'est un sous groupe donc monogène et le ppcm est le générateur positif(plus petit élément positif strictement également ) d'où le résultat manquant.
 par legeniedesalpages » 02 Mar 2008, 20:04
par legeniedesalpages » 02 Mar 2008, 20:04
alavacommejetepousse a écrit:bonsoir
l'ensemble des multiples (relatifs)de p est le sous groupe engendré par p
l'ensemble des multiples communs de p et q est l'intersection des deux sous groupes c'est un sous groupe donc monogène et le ppcm est le générateur positif(plus petit élément positif strictement également ) d'où le résultat manquant.
ok mais en fait je me posais cette question, justement dans le but de montrer après que
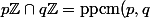\mathbb{Z})
.
J'ai montré que
\mathbb{Z}\subset p\mathbb{Z}\cap q\mathbb{Z})
, mais pour l'autre inclusion je ne vois pas.
 par alavacommejetepousse » 02 Mar 2008, 20:28
par alavacommejetepousse » 02 Mar 2008, 20:28
en notant m le générateur positif de l'intersection
on a m multiple commun de p et q donc supérieur à ppcm
et comme ppcm est dans l'intersection, ppcm est un multiple de m donc m = ppcm.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités