Question en math

[mathieusar]

Salut

je cherche une fonction[ f(x) pour tout x f (x) > (1/x) et telle que sa primitive soit nulle en x=0]
merci

[arnaud32]

pour tout x tu as f(x)>1/x ? ca donne quoi ca en x=0?

[mathieusar]

pour tout x strictement positive , f (x)>1/x ,, mais la primitive de f est deffinie en zero et egale a zero en x=0, je cherche alors une fonction f qui verifie ces conditions

[arnaud32]

si tu notes F ta primitive
que peux tu dire de F(x)-F(1)?

[mathieusar]

bonjour

que se soit la résultat de F(x)-F(1) ; mais ce qui est important pour moi est que la limite de F quand x tend vers zeros soit egal à zeros

[deltab]

Bonjour

bonjour

que se soit la résultat de F(x)-F(1) ; mais ce qui est important pour moi est que la limite de F quand x tend vers zeros soit egal à zeros

.

Le problème n'est pas au niveau de la primitive F. Si une des primitives est continue en 0, on peut alors choisir la constante d'intégration de telle manière à avoir F(0)=0. Que dis-tu de la fonction définie par , sur 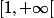, par exemple (constante) .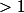
Prends alors et 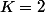. Peux-tu alors construire une primitive continue sur vérifiant